Этот несовершенный мир 🌎
По мере того как мы углубляемся в своих знаниях – мы теряем способность адекватно оценивать насколько сложны наши логические выкладки для неподготовленного слушателя. Вещи, которые нам кажутся очевидными и само собой разумеющимися, не кажутся таковыми для тех, кто далек от темы обсуждения. Всякий раз когда я завожу разговор с людьми от бизнеса о том, что все происходящее вокруг нас имеет вероятностную природу, то сталкиваюсь со стеной непонимания. Бизнес не терпит размышлений в формате нулевая гипотезу должна быть отвергнута для p-value 0.01, в бизнесе план выполнен или не выполнен, задача сделана или не сделана. Бизнесу важно ощущать четкость сродни простой армейской конструкции: заметил что-то? тогда, если движется – застрели, иначе – покрась.
Ситуация также осложняется тем, что люди бизнеса постоянно куда-то спешат, торопятся и у них совершенно отсутствует время на то чтобы погружаться в тонкости описания окружающего мира. К сожалению, Data Science проекты не могут обходится простыми конструкциями и возникает необходимость делать экспресс-погружение в теорию вероятности за 3 минуты ⌛️
Думаю, хорошая визуализация – это ключ к пониманию многих вещей. Наиболее распространенным способом визуализации меры неопределенности в теории вероятности – является построение диаграммы распределения т.е. гистограммы. Конечно это далеко не единственный способ, но наверное самый распространенный в сфере науки, но к сожалению едва популярный в сфере бизнеса потому как такая визуализация требует некоторого погружения в предмет. Далее я построю простую аналогию, которая позволяет достаточно быстро добиться понимания того, что изображено на диаграммах распределения 📊
Про гольф и бизнес 🏌🏾
Все мы знаем как серьезный бизнес любит решать свои вопросы на поле для гольфа. Я пойду дальше и сделаю допущение, что бизнес сводится к этой игре и менеджмент – это гольфист, которому нужно попасть в лунку одним ударом. Также допустим, что гольфист, если не знает, то догадывается какая траектория полета должна быть чтобы попасть в лунку. Я будут упрощать свою модель и вместо двумерной модели поля для гольфа буду использовать одномерную, имея ввиду, что двумерный вариант можно получить просто умножением на два. Известно, что мяч будет лететь дальше при наклоне удара в 45 градусов, если не учитывать силу ветра. Естественно, попасть в лунку достаточно непросто в силу ряда обстоятельств:
- Начальная скорость удара может отличаться от той, которая предположительно необходима для попадания в лунку
- Угол удара также может отличаться от того, который был запланирован изначально
- Также существует ветер, который может существенно повлиять на скорость и траекторию мяча и который мы не контролируем – это некая внешняя сила и с ней приходится мириться как с данностью
- Наконец, траектория может ыть выбрана не вполне корректно т.е. мяч будет падать с некоторым смещением от лунки
Важно отметить, что указанные обстоятельства связаны с тем как исполняется заявленный план т.е. как хорошо гольфист отправляет мяч по заданной, возможно даже математически рассчитанной траектории. Естественно, в реальной жизни плановая траектория может быть рассчитана неверно т.е. со смещением. В таких случаях можно уверенно говорить о том, что план был неверный. В действительности очень сложно дать ответ на вопрос: был ли неправильно составлен план или же исполнение было на низком уровне т.к. бизнес-процессы могут попадать под влияния множества факторов, что делает невозможным повторение эксперимента, как это возможно с ударом гольфиста. Более того, часто планы принято формировать со смещением для того чтобы усилить мотивацию исполнителей на лучшие показатели 🥕
Хорошо, после краткой вводной предлагаю вооружиться базовыми знаниями физики и формализовать модель гольф-бизнеса в виде системы уравнений движения мяча:
, где
- – начальная скорость в проекции на землю
- – начальная скорость в проекции, перпендикулярной земле
- – коэффициент сопротивления воздуха
- – постоянная силы притяжения
Почему я могу записать эту систему уравнений именно в таком, а не каком-либо ином виде? Дело том, что описанные уравнениями зависимости могут быть достаточно просто подтверждены экспериментальным образом. К сожалению, то что работает в физике не работает в экономике или работает, но несколько по иному. Я выбрал этот пример для наглядности и также для формирования уверенности в том, что многие бизнес-решения можно и нужно рассчитывать аналогично тому как это делается в точных науках.
После простых преобразований:
В целом, этого достаточно для моделирования траектории полета мяча численным методом. Между тем вполне возможно решить такую систему уравнений как оптимизационную задачу. Например, можно аналитически вычислить оптимальный угол полета мяча для минимальной начальной скорости, что звучит логично, если принимать во внимание, что с ростом силы удара может падать точность.
Модель гольф-бизнеса ⛳️
Прежде чем стартовать моделирование необходимо сделать подготовительные упражнения:
library(thematic) # пакет для автоматической установки стилей графиков
library(tidyverse) # набор пакетов по принципу "все включено", в который включен ggplot2
library(ggpp) # расширение для ggplot2
# Активируем тему для блога
thematic_rmd(bg = "#1D1E20", accent = "cyan", fg = "grey90", font = font_spec("Roboto"),
sequential = firatheme::firaPalette(100),
qualitative = palette.colors(palette = "Tableau"))
# Сохраняем палитру в отдельную переменную
my_pal <- palette.colors(palette = "Tableau") %>% unname()
golfer <- magick::image_read_svg("golfer.svg") # картинка гольфиста
hole <- magick::image_read_svg("hole.svg") # картинка лунки
Пусть лунка будет находится на расстоянии 50 м от гольфиста. Далее нужно подставить в формулы значения, которые позволят попасть в цель: пока без учета случайных факторов, которые могут влиять на траекторию полета:
alpha <- pi/4 # мяч летит под углом 45'
g <- 9.8 # постоянная земного притяжения
k <- 2 # коэффициент сопротивления ветра
V = 55 # начальная скорость полета мяча
Vx = V*cos(alpha) # проекция скорости на горизонтальную ось
Vy = V*sin(alpha) # проекция скорости на вертикальную ось
# Модельная траектория полета мяча для 100 точек
dt <- tibble(t = 0:100/10, x = Vx*t/(1+k), y = Vy*t - g*(t^2))
# Визуализация траектории
filter(dt, y > 0) %>%
ggplot(aes(x, y, size = t)) +
annotate("text_npc", npcx = .5, npcy = .5, alpha = .9, size = 15, # для брендирования
label = "InvestCookies.ru", color = "#1D1E20") + # для брендирования
geom_point(alpha = .3, alpha = .02, col = my_pal[2]) +
scale_size(range = c(0, 20)) +
geom_hline(yintercept = 0, col= "black") +
ylim(-5, 50) +
scale_x_continuous(breaks = (0:10)*10, labels = (0:10)*10, limits = c(-5, 100)) +
labs(title = "Исполнение четко согласно плану", y = "Высота, м.", x = "Расстояние до лунки, м.")+
theme(legend.position = "none") +
annotation_custom(grid::rasterGrob(golfer), xmin = -10, xmax = 10, ymin = 0, ymax = 20) +
annotation_custom(grid::rasterGrob(hole), xmin = 45, xmax = 55, ymin = -1, ymax = 10)
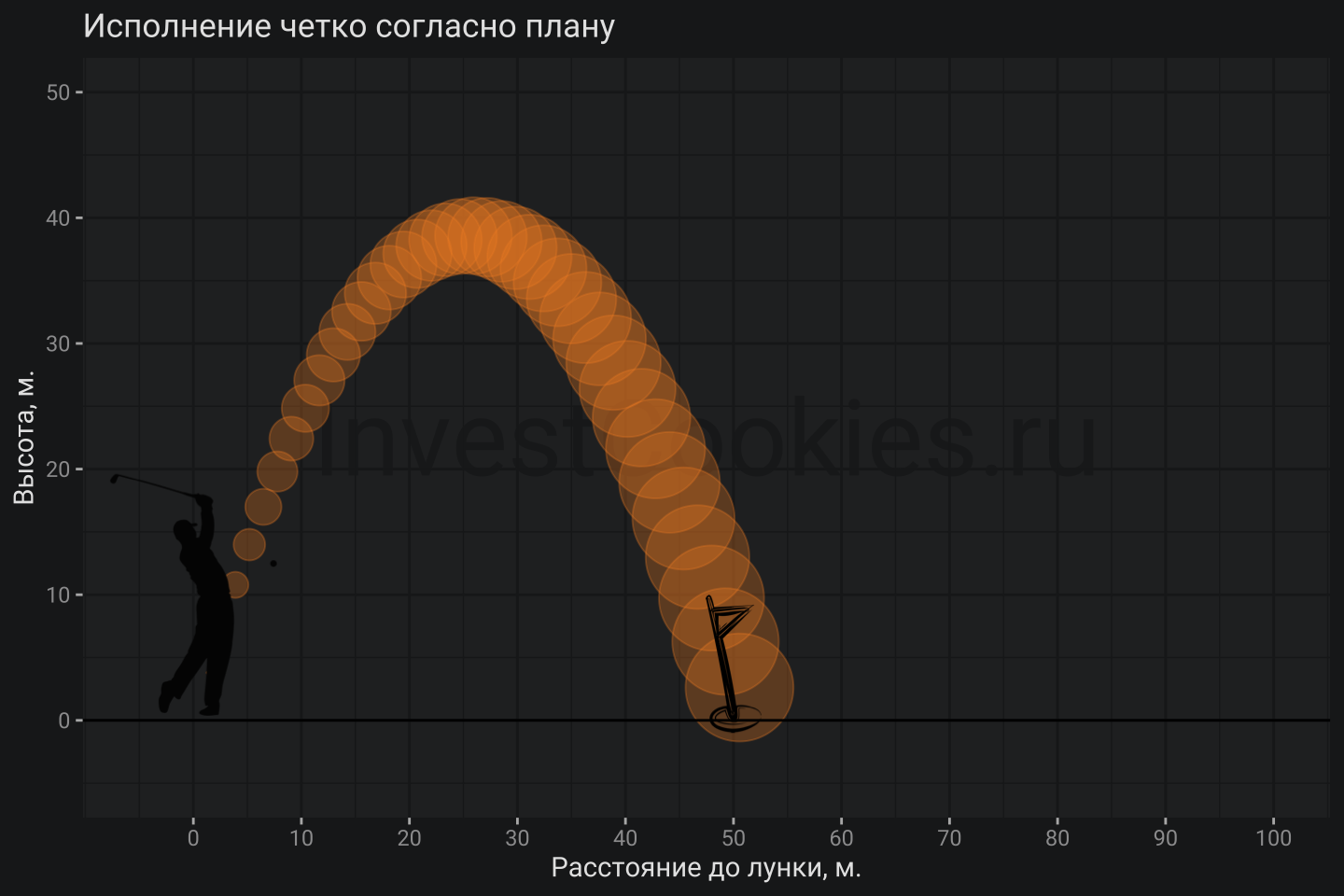
Далее будет смоделирована серия ударов хорошего мастера, который достаточно уверен в себе чтобы не сбивать прицел и методично отрабатывать удары, на которые влияют случайные факторы внутреннего и внешнего характера:
n <- 500 # количество попыток
set.seed(123)
alpha <- rnorm(n, pi/4, pi/12) # угол 45' с дисперсией 15'
k <- rnorm(n, 2, .5) # коэффициент сопротивления ветра с отклонениями 0.5
V <- rnorm(n, 57.5, 1) # начальная скорость полета мяча с отклонением 5 м/с
Vx <- V*sin(alpha) # проекция скорости на горизонтальную ось
Vy <- V*cos(alpha) # проекция скорости на вертикальную ось
# Таблица параметров траекторий для всех попыток n
dt_mdl1 <- tibble(k = k, Vx = Vx, Vy = Vy)
# Таблица траекторий для всех попыток n
res1 <- pmap_dfr(dt_mdl1, ~ tibble(t = 0:100/10, x = ..2*t/(1 +..1), y = ..3*t - g*(t^2)), .id = "id") %>%
filter(y >=0) %>%
mutate(scenario = "Профи")
# Таблица распределения попаданий
res_distr1 <- group_by(res1, id) %>%
summarise(last = max(x))
# Функция построения графика, которая будет пере использоваться
plot_trajectory <- function(mdl_df, distr){
ggplot(mdl_df) +
annotate("text_npc", npcx = .5, npcy = .5, alpha = .9, size = 15, # для брендирования
label = "InvestCookies.ru", color = "#1D1E20") + # для брендирования
geom_histogram(data = distr, aes(last), bins = 11, alpha = .5) +
geom_point(aes(x, y*2.5, size = t), alpha = .02, col = my_pal[2]) +
geom_hline(yintercept = 0, col = "black") +
scale_y_continuous(sec.axis = sec_axis(~./2.5, name = "Высота, м."), expand = c(.1, 0)) +
scale_x_continuous(breaks = (0:11)*10, labels = (0:11)*10, limits = c(0, 115)) +
annotation_custom(grid::rasterGrob(golfer), xmin = -20, xmax = 20, ymin = 0, ymax = 40) +
annotation_custom(grid::rasterGrob(hole), xmin = 45, xmax = 55, ymin = -1, ymax = 20) +
labs(y = "Количество мячей в корзине, шт.", x = "Расстояние до лунки, м.") +
theme(legend.position = "none")
}
plot_trajectory(res1, res_distr1) + ggtitle("Исполнение плана мастером")
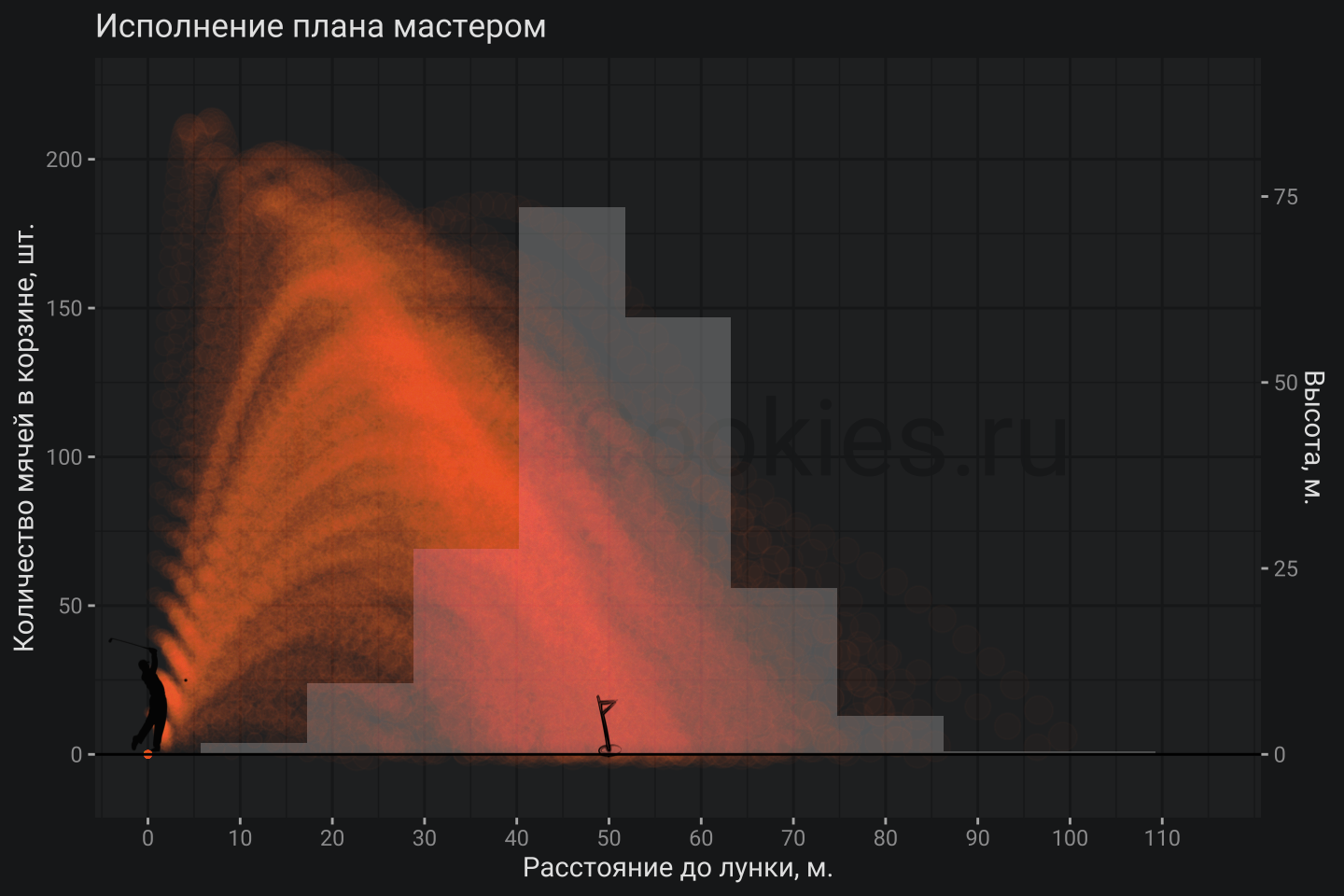
Можно заметить, что далеко не все 500 попыток были успешными, но в среднем мяч попадал в лунку. Конечно ветер и твердость руки могли иногда подводить, но уверенность в правильности траектории и методичное исполнение плана дают весьма хороший результат. Видимо такая работа менеджмента может сопровождаться эпитетом: уверенно идут к своей цели.
Предлагаю представить, что на каждой отсечке по 10 м стоит огромная корзина диаметром 10 м, в которую попадают мячи и по результатам всех попыток существует возможность посчитать какое количество мячей оказалось в каждой корзине 🗑
Теперь можно построить диаграмму со столбиками, которые будет соответствовать количеству посчитанных мячей в каждой корзине – это и будет диаграмма распределения 500 попаданий Вот собственно и вся аналогия 🥸
Далее будет смоделирована ситуация с неопытным исполнителем:
set.seed(123)
alpha <- rnorm(n, pi/4, pi/10) # угол 45' с дисперсией 30'
k <- rnorm(n, 2, .5) # коэффициент сопротивления ветра с отклонениями 0.5
V <- rnorm(n, 57.5, 2) # начальная скорость полета мяча с отклонением 10 м/с
Vx <- V*sin(alpha) # проекция скорости на горизонтальную ось
Vy <- V*cos(alpha) # проекция скорости на вертикальную ось
# Таблица параметров траекторий для всех попыток n
dt_mdl2 <- tibble(k = k, Vx = Vx, Vy = Vy)
# Таблица траекторий для всех попыток n
res2 <- pmap_dfr(dt_mdl2, ~ tibble(t = 0:100/10, x = ..2*t/(1 +..1), y = ..3*t - g*(t^2)), .id = "id") %>%
filter(y >=0) %>%
mutate(scenario = "Любитель")
# Таблица распределения попаданий
res_distr2 <- group_by(res2, id) %>%
summarise(last = max(x))
plot_trajectory(res2, res_distr2) + ggtitle("Исполнение плана любителем")
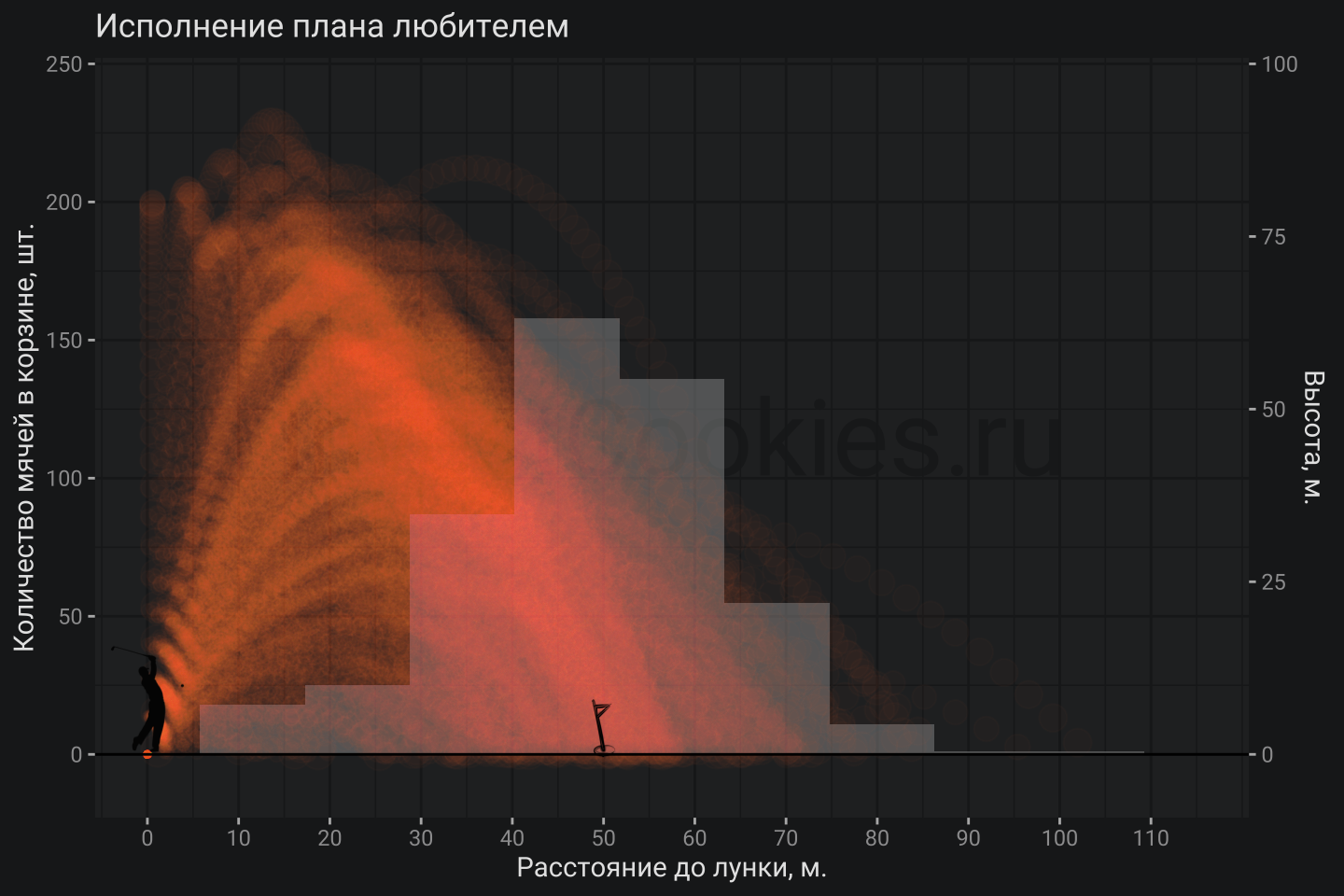
В данном случае нестабильность силы удара и блуждание по углу существенно увеличили разброс падения мяча. Это не значит, что попаданий не было: они были, но вот количество таких попаданий было не очень велико, хотя наибольшее количество падений мяча наблюдается именно в зоне нахождения лунки. Другими словами, план у любителя был хороший, а вот исполнение было не очень.
Теперь будет смоделирована ситуация при которой работает гольфист-максималист, который планирует траекторию удара со смешением, прилагая больше усилий чем того требует ситуация:
set.seed(123)
alpha <- rnorm(n, pi/4, pi/12) # угол 45' с дисперсией 15'
k <- rnorm(n, 2, .5) # коэффициент сопротивления ветра с отклонениями 0.5
V <- rnorm(n, 57.5, 1) + 10 # начальная скорость полета мяча с отклонением 5 м/с
Vx <- V*sin(alpha) # проекция скорости на горизонтальную ось
Vy <- V*cos(alpha) # проекция скорости на вертикальную ось
# Таблица параметров траекторий для всех попыток n
dt_mdl3 <- tibble(k = k, Vx = Vx, Vy = Vy)
# Таблица траекторий для всех попыток n
res3 <- pmap_dfr(dt_mdl3, ~ tibble(t = 0:100/10, x = ..2*t/(1 +..1), y = ..3*t - g*(t^2)), .id = "id") %>%
filter(y >=0) %>%
mutate(scenario = "Максималист")
# Таблица распределения попаданий
res_distr3 <- group_by(res3, id) %>%
summarise(last = max(x))
plot_trajectory(res3, res_distr3) + ggtitle("Исполнение плана максималистом")
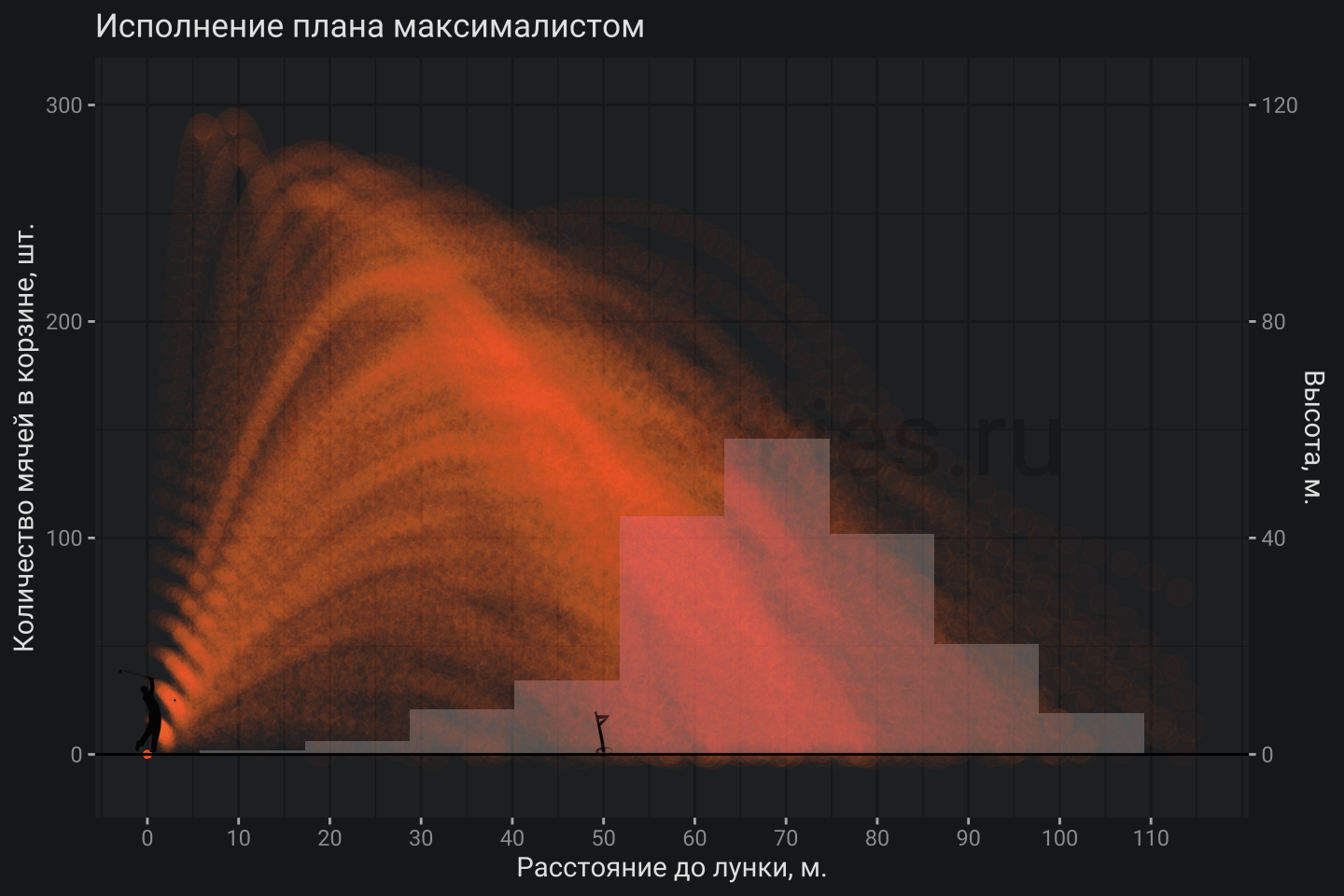
В данном случае большинство попаданий находится на отметке 65 м, что означает перелет. В плане полета мяча присутствует явное смещение, что требует корректировки т.е. в данном случае можно сказать, что планирование осуществлено не качественно.
В такой ситуации мне скажут: Что за бред? у нас реальный бизнес, а не игрушки! поэтому чем больше продажи – тем лучше, чем больше объем производства – тем лучше!. В действительности все имеет свои предельные мощности т.е. можно много продать, но логистика не справиться с объемами перевозок, также много можно произвести, но складских мощностей будет не достаточно и следовательно товар может испортится без надлежащих условий хранения. Пределы существую всегда и нужно всегда помнить когда они вступят в игру и станут определяющим фактором.
Качество и правило трех (\sigma)
Теперь когда стало понятно, что из себя представляет диаграмма распределения и почему важно к ней обращаться нужно затронуть тему качества. Качество вопреки расхожему мнению – это не сравнительная характеристика т.е. когда мы говорим плохое качество или хорошее качество – мы скорее говорим глупости. Качество – это уровень, которому продукт или изделие должно соответствовать. Уровень соответствия – это стандарт качества. Браком соответственно называется те изделия, которые этому стандарту качества не соответствуют. В данной терминологии совершенно не важно о каком продукте идет речь: о компьютерных чипах, сахарном песке или машинках на батарейках. Очевидно, что большое количество брака – это плохо для бизнеса, но совсем без брака не бывает т.к. всегда существует какие-то факторы, которые нет возможности контролировать как в примере про гольф. Какое же количество брака является приемлемым? Тут на арену как раз выходит правило трех (\sigma) т.е. считается, что если характеристика в 99,72% случаях соответствует стандартам качества, то такое процесс производства – является качественным. 99,72% – это три среднеквадратичных отклонения. В примере с гольфом три (\sigma) будут следующие:
med <- median(res_distr1$last) %>% round(2)
sd <- round(sd(res_distr1$last)*3, 2)
c(med - sd, med + sd) # стандарт качества для мастера
## [1] 11.57 89.51
Теперь можно четко сказать, что мастером гольфа становятся те игроки, которые в 99,72% случаях попадают диапазон от 11 м до 90 м, а у новичков такой диапазон будет естественно больше:
med <- median(res_distr2$last) %>% round(2)
sd <- round(sd(res_distr2$last)*3, 2)
c(med - sd, med + sd) # стандарт качества для новичка
## [1] 2.89 95.27
Игроки со смещенным планом полета мяча получат смещенный диапазон попаданий, но более интересно то, что разброс приземлений мяча также увеличивается:
med <- median(res_distr3$last) %>% round(2)
sd <- round(sd(res_distr3$last)*3, 2)
c(med - sd, med + sd) # стандарт качества для максималиста
## [1] 16.17 123.43
Теперь на основе теории вероятности можно сделать объективный вывод о том, что гольфист-максималист должен поправить свою плановую траекторию. Для этого необходимо доказать, что смещение попаданий от лунки не носит случайный характер. В первую очередь нужно убедиться, что распределение падений мяча гольфиста-макималиста имеет нормальную форму:
shapiro.test(res_distr3$last)
##
## Shapiro-Wilk normality test
##
## data: res_distr3$last
## W = 0.98843, p-value = 0.0005427
К сожалению, распределение не получилось нормальным поэтому для проверки гипотезы о том, что игрок изначально правильно планирует траекторию полета мяча необходимо использовать вместо классического теста Стьюдента параметрический аналог – тест Манна-Витни. Вот, что получается для профи:
wilcox.test(res_distr1$last, mu = 50, conf.level = 99.72)
##
## Wilcoxon signed rank test with continuity correction
##
## data: res_distr1$last
## V = 64573, p-value = 0.5468
## alternative hypothesis: true location is not equal to 50
Значимость высокая и следовательно можно не отвергать нулевую гипотезу о том, что попадания гольфиста приходятся на 50 м.
wilcox.test(res_distr3$last, mu = 50, conf.level = 99.72)
##
## Wilcoxon signed rank test with continuity correction
##
## data: res_distr3$last
## V = 117417, p-value < 2.2e-16
## alternative hypothesis: true location is not equal to 50
Значимость низкая и следовательно можно отвергнуть нулевую гипотезу о том, что попадания гольфиста приходятся на 50 м.
Вот таким слегка замысловатым образом можно осуществлять оценки того, где находится проблема: либо планы составлены некорректно, либо исполнение плана требует улучшений.
Реальный кейс 💼
Не хотелось бы заканчивать свое повествование описанием виртуальных примеров, а добавить немного реальной практики, да такой которая бы касалась всех без единого исключения. Пожалуй возьму цифры по исполнению федерального бюджета РФ:
budget <- readxl::read_excel("data/fedbud_month.xlsx", skip = 2, sheet = 3) %>%
filter(`РАЗДЕЛ I` == "Дефицит (-)/Профицит (+)") %>%
select(-(1:2)) %>%
t() %>%
.[, 1] %>%
as_tibble() %>%
mutate(year = c(rep(2011:2021, each = 12), rep(2022, 5)), # индекс годов
month = c(rep(1:12, times = 11), 1:5)) %>% # индекс месяцев
group_by(year) %>%
mutate(change = value - lag(value, default = 0), # изменение баланса т.к. исходные данные даны накопленным итогом по году
status = if_else(month == 12, "декабрь", "прочее")) # раскрашивалка месяцев
ggplot(budget) +
annotate("text_npc", npcx = .5, npcy = .5, alpha = .9, size = 15, # для брендирования
label = "InvestCookies.ru", color = "#1D1E20") +
geom_histogram(aes(change, fill = status), alpha = .4, bins = 20) +
geom_vline(aes(xintercept = median(budget$change), linetype = "медиана")) +
geom_vline(aes(xintercept = mean(budget$change), linetype = "среднее")) +
scale_linetype_manual(values = c("медиана" = 5, "среднее" = 1)) +
labs(title = "Распределени дефицитов(-)/профицитов(+) федерального бюджета РФ", fill = "", lty = "", y = "Количество наблдений", x = "Дефицит/профицит",
caption = "Источник: Минфин РФ")
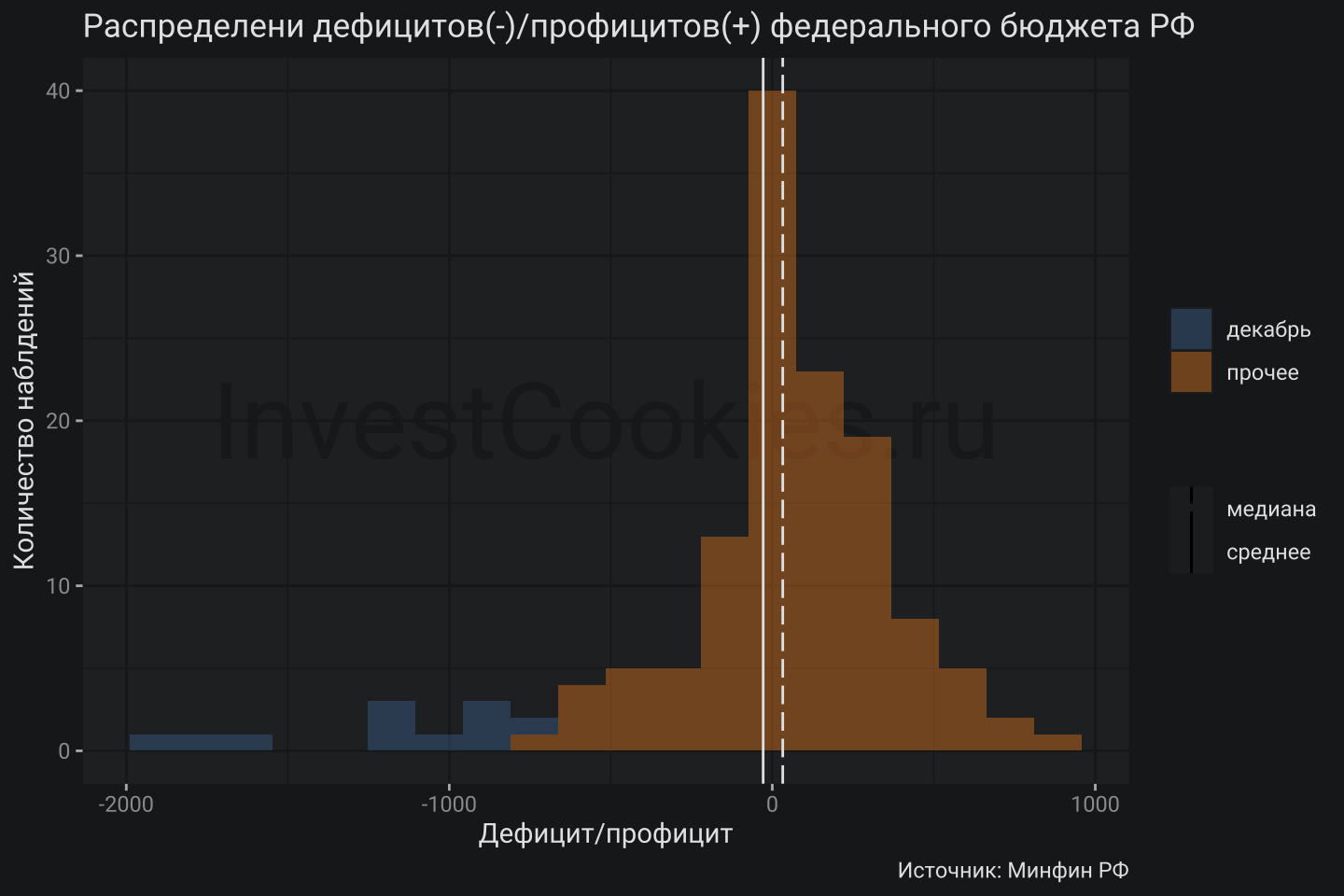
В данном примере можно заметить, что самые большие дефициты бюджета случаются в декабре месяце каждого года, отражая неравномерность расходования средств. В среднем федеральный бюджет закрывался с небольшим минусом в последние 11 лет в размере -0.21 млрд. рублей ежемесячно. В целом можно сказать, что бюджет планируется достаточно хорошо с точки зрения финансового баланса расходов/доходов, но неравномерность исполнения бюджета требует доработок.
Итоги
Некоторые итоги:
- Мир вокруг нас носит вероятностную природу и ему плевать на то как мы его понимаем. Бизнес хочет понимать мир в упрощенной форме и ему можно и нужно в этом помогать 🦮
- Вероятностную природу мира очень удобно представлять в виде диаграмм распределений или гистограмм, которые способны прояснить качество планирования и качество исполнения планов 📋
- Качество – это соответствие изделия или процесса определенному уровню. Когда речь заходит про производственный процесс, то можно говорить о соответствии процесса норме полезного выхода в рамках концепции трех (\sigma)(\sigma)(\sigma)
- Иногда статистические методы позволяет выяснить в какой ситуации менеджмент плохо планирует, а в какой ситуации плохо исполняет планы 🤓
- Реальный кейс федерального бюджета РФ: неплохо планируется, но исполняется неравномерно, особенно в декабре 💸
Простой способ узнать о новых публикациях – подписаться на Telegram-канал: