Предыстория
Люди любят прогнозировать и занимаются этим каждый день, иногда даже не осознавая того чем занимаются. Каждый день мы планируем поездку на работу 🚗 и нам приходится оценивать время, которое нам потребуется для того чтобы прибыть вовремя. Кто-то делает поправки на погодную обстановку или сезонные особенности: все обращали внимание, что летом на дорогах посвободнее, а в канун нового года твориться беспробудная жесть. Прокручивая такие факторы в голове мы занимаемся чем-то вроде факторного анализа. Подготовленный читатель может возразить, что “все вы врете!!! факторный анализ - это метод главных компонент и точка!!!” Формально подготовленный читатель будет прав, хотя наличие или отсутствие формальной математической записи модели прогнозирования еще не делает прогноз плохим или хорошим. На любом производстве можно найти условного технолога-Михалыча, который на глазок шикарно определяет способы повышения выхода продукции заданного качества, а все попытки заменить технолога-Михалыча супер-инновационным и мега-дорогим программным обеспечением - терпят крах, хотя конечно бывает и наоборот. Получается, что модель, формируемая в нашей голове на базе нашего опыта может быть вполне приемлемой, несмотря на отсутствие формального математического выражения, которое ее описывает.
С технологом-Михалычем мы разобрались: он десятками лет оттачивал свой навык на производстве и его авторитет непререкаем, на нем можно сказать держится все производство. Но то, что позволено технологу-Михалычу, то не позволено датасантисту, особенно молодому. И это плохая новость для датасантиста, который прослушал курс приблизительно в следующем содержании:
- Вот переменные независимые, а вот переменная зависимая, которую нужно предсказать
- Бывает проблема, что значения пропущены – вот так с этим нужно работать…
- Вот алгоритм нейронной сети, а вот алгоритм решающих деревьев - они работают как-то так и они все очень крутые
- Вы можете столкнуться с переобучением и еще страшнее с утечкой данных – data leakage, поэтому вот вам кросс-валидация и методы изоляции данных
- Вот еще можно делать ансамбли и это вообще космос 🪐
Как-то так, очень технологично и очень эффективно, если задача сформулирована таким образом чтобы алгоритм ее смог эффективно обуздать. Собственно практически весь эмпирический опыт датасантист вкладывает в так называемый этап “feature engineering” – это что-то вроде способа переложить эмпирические знания человека в пространство признаков для того чтобы алгоритм смог эффективно использовать не только сырые данные, но и опыт исследователя.
Уже пошел далеко не первый год как я занимаюсь коммерческой разработкой прогнозных моделей и в каждой новой задаче я пытаюсь добавить осмысленности тому чем занимаюсь, связывая различные дисциплины и практики в единую логическую систему. Я попробую показать как прикладной математический аппарат, применяемый в физике может сделать прогнозную модель более точной, а главное осмысленной.
Мы будем строить прогнозную модель для выручки нового барбершопа сети барбершопов 🧔🏻️. Почему барбершопа? Просто потому что- - это модно. На самом деле тут нет особой разницы: это могут быть рестораны быстрого питания, производственный комплекс или что-то еще. Впервые с подобной задачей я столкнулся около пяти лет назад при разработке модели прогноза для крупного производства с миллиардными инвестициями. В 2020 году этот подход был представлен на конференции Прогнозирование и планирование, который я хотел бы разобрать в более подробном формате.
Постановка задачи
Пусть у нас имеется сеть барбершопов из двух уже открытых заведений и одного-планируемого к открытию. В нашем распоряжении имеется история некоторой динамики выручки для двух первых барбершопов. Соответственно мы хотим сделать прогноз выручки для третьего нового барбершопа. К сожалению, использовать реальные данные заказчика будет не этично по отношению к их владельцу, поэтому для нашего примера мы просто синтезируем данные, которые будут очень похожи на оригинал. Тут придется поверить на слово, что они действительно похожи.
library(thematic)
library(echarts4r)
library(tidyverse)
library(ggpp)
library(rsample)
library(broom)
library(DT)
# Настройка всякой красоты
my_pal <- palette.colors(palette = "Tableau") %>% unname()
e_common(font_family = "Verdana", theme = "infographic")
sysfonts::font_add_google("Roboto")
thematic_rmd(bg = "#1D1E20", accent = "cyan", fg = "grey90", font = font_spec("Roboto"), sequential = firatheme::firaPalette(100), qualitative = firatheme::firaPalette(50))
# Генерация данных
day <- 1:540 # указываем интервал времени в днях
Ta <- 150 # устанавливаем время разгона, который в дальнейшем будем искать
Lu <- 12 # устанавливаем предельную выручку на одно кресло барбершопа в день, тыс. руб.
power_bshop1 = 4*Lu # первый барбершоп только с четырьмя креслами
power_bshop2 = 6*Lu # второй барбершоп с шестью креслами
power_bshop3 = 9*Lu # третий барбершоп с девятью креслами
week_pattern = c(0.5, 0.6, 0.6, 0.6, 0.7, .9, .8)
RF <- 15 # стохастический фактор
set.seed(123) #устанавливаем метку генерации случайных чисел для стабильного воспроизводства результатов
sim_bshop <- tibble(day_num = day, # добавляем номер дня
week_effect = c(1, rep(week_pattern, 77)), # синтезируем периоды остановов производства на обслуживание
week_n = c(0, rep(1:77, each = 7)),
bshop1 = (power_bshop1*(1-exp(-day/Ta)) + rnorm(day, 0, power_bshop1/RF))*week_effect, # данные для барбершопа 1
bshop2 = (power_bshop2*(1-exp(-day/Ta)) + rnorm(day, 0, power_bshop2/RF))*week_effect, # данные для барбершопа 2
bshop3 = (power_bshop3*(1-exp(-day/Ta)) + rnorm(day, 0, power_bshop3/RF))*week_effect) %>% # данные для барбершопа 3
mutate(across(-day_num, ~if_else(. < 0, 0, .))) # обнуляем отрицательные значения
# Красивый график - это всегда полезно!!!
e_charts(sim_bshop, day_num) %>%
e_line(bshop1, itemStyle = list(borderColor = NULL, opacity = .5),
lineStyle = list(opacity = .5), color = my_pal[1], name = "Барбер 1") %>%
e_line(bshop2, itemStyle = list(borderColor = NULL, opacity = .5),
lineStyle = list(opacity = .5), color = my_pal[2], name = "Барбер 2") %>%
e_loess(bshop1 ~ day_num, lineStyle = list(type = "dashed", width = 3),
emphasis = list(focus = 'self'), showSymbol = FALSE, color = my_pal[1], name = "Тренд 1") %>%
e_loess(bshop2 ~ day_num, lineStyle = list(type = "dashed", width = 3),
emphasis = list(focus = 'self'), showSymbol = FALSE, color = my_pal[2], name = "Тренд 2") %>%
e_mark_line(serie = "Барбер 1", title = "Мощность 1", data = list(yAxis = 48)) %>%
e_mark_line(serie = "Барбер 2", title = "Мощность 2", data = list(yAxis = 72)) %>%
e_datazoom(x_index = 0, type = "slider") %>%
e_tooltip(trigger = "axis", digits = 0, textStyle = list(color = "white"), axisPointer = list(type = "line"),
formatter = htmlwidgets::JS("function (param) {
let param1 = param[1];
let param2 = param[0];
return [
'<b>День</b>: ' + param1.value[0] + '<hr size=1>',
'<b>Барбершоп 1</b>: ' + Math.round(param1.value[1]) + ' тыс. руб.' + '<br/>',
'<b>Барбершоп 2</b>: ' + Math.round(param2.value[1]) + ' тыс. руб.' + '<br/>',
].join('');}")) %>%
e_title(text = "Динамика выручки барбершопов") %>%
e_y_axis(name = "Выручка, тыс. руб.") %>%
e_x_axis(name = "День") %>%
e_legend(type = "scroll", selector = TRUE, padding = 30) %>%
e_draft("InvestCookies.ru", size = "80px", opacity = 0.4)
Получились два графика с некоторым случайными блужданиями и с
учетом недельного паттерна, а также с учетом некого уровня насыщения,
который можно попробовать разглядеть на сглаженных кривых, обозначенных как
Тренд.
Сходу напрашивается вариант аппроксимировать тренд какой-либо функцией: логарифмом или кусочным полиномом (сплайном). Такая аппроксимация вполне возможна, но на достаточно больших значениях прогноз будет существенно расходится с ожиданиями того, что должно быть.
Опыт и знания
Опыт открытия барбершопов подсказывает следующее:
- Дневная выручка имеет ограничение сверху, что связано ограничение на количество мест для посетителей
- Выручка на первых этапах растет интенсивнее чем на этапах близких к насыщению
- Стартовая скорость определяет время разгона выручки и характеризует то насколько хорошо выбрана локация и проведена маркетинговая компания
Собственно три тезиса выше определяют набор параметров, которые теперь хорошо бы транслировать в формальное математическое выражение. Так как речь идет о динамическом процессе во времени, то разумно предположить, что этот процесс будет хорошо описываться дифференциальным уравнением, например, таким:
$$ T_{a}⋅\dot{r} + r = Q $$
- (T_{a}) - время разгона, которое геометрически может быть интерпретировано как интервал, полученный отсечением оси времени проекцией от точки пересечения касательной кривой выручки и уровня мощности… бррр 🤯 лучше посмотреть картинку ниже
- (r) - искомая переменная выручки
- (Q) - предельная (теоретическая) мощность барбершопа
triangle <- tibble(x = c(0, 100, 100), y = c(0, 100, 0))
ggplot(triangle) +
annotate("text_npc", npcx = .5, npcy = .5, label = "InvestCookies.ru", color = "#1D1E20", alpha = .9, size = 20) +
geom_function(fun = ~100*(1-exp(-./150)), color = my_pal[1]) +
geom_segment(aes(x = 0, y = 0, xend = 100, yend = 100), linetype = 5) +
geom_function(fun = ~100, linetype = 5) +
geom_segment(aes(x = 100, y = 100, xend = 100, yend = 0), linetype = 5) +
geom_segment(aes(x = 0, y = 0, xend = 100, yend = 0), linetype = 5, arrow = arrow(length = unit(0.03, "npc"), ends = "both"), col = my_pal[2]) +
geom_polygon(aes(x = x, y = y), alpha = .2, fill = my_pal[1]) +
annotate("text", x = 50, y = 10, label = "Ta", color = my_pal[2], size = 8) +
annotate("text", x = 400, y = 110, label = "Q", color = my_pal[1], size = 8) +
xlim(0, 400) +
ylim(0, 120) +
labs(y = "Выручка | Выпуск | Объем производства", x = "Время") +
theme(axis.title.y = element_text(color = my_pal[1]))
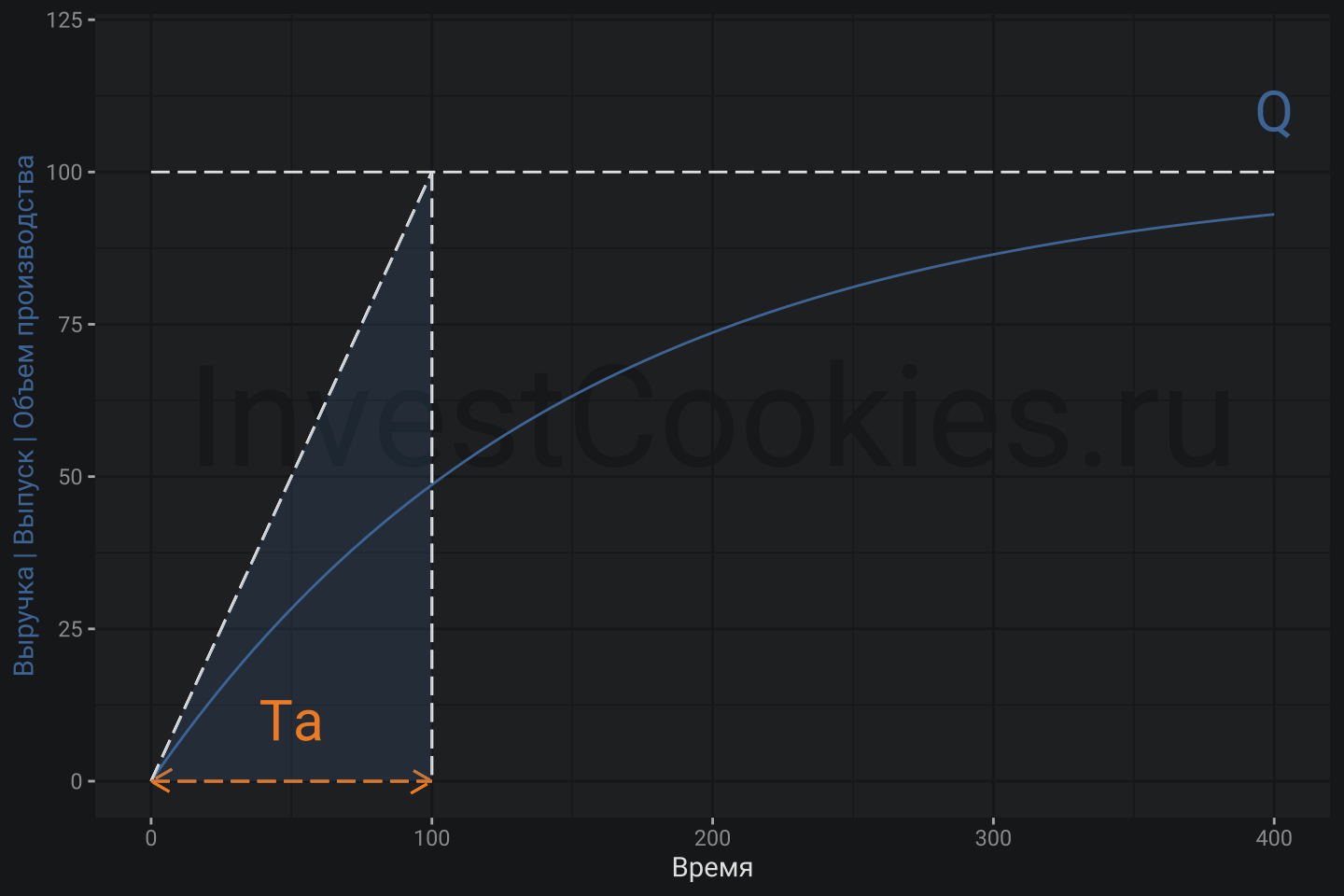
Интуитивно можно заметить, что большие значения (T_{a}) - увеличивает кривизну кривой и ускоряют выход показателя выручки на предельные значения, ограниченные мощностью. Рассмотрим краевые значения. В самом начале в момент (t_{0} = 0) имеется (r = 0) и следовательно: $$ \dot{r} = \frac{Q}{T_{a}} $$ что ведет к геометрической интерпретации (T_{a}). Действительно, производная функции кривой – это тангенс угла касательной к кривой, где (T_{a}) - прилежащий катет. Далее, при (t_{max}) имеется: $$ r \approx 400 \Rightarrow \dot{r} \approx 0\ $$ означает, что скорость роста выручки замедлилась до нуля. Другими словами, рассмотрение краевых точек позволяет эмпирически записать дифференциальное уравнение выше и если это удалось сделать, то будет логично его решить. Собственно почему бы не вспомнить курс дифференциального исчисления? 🥸
Прежде всего, производим замену (r = uv), представляя искомую функцию в виде произведения переменных: $$ r'=u'·v+v'·u $$
и получаем: $$ T_{a}(u'·v+v'·u)+ uv = Q $$
Далее решается два совместных уравнения:
$$ T_{a}v' + v = 0,\nobreakspace T_{a}u'·v = Q $$
Первое уравнение: $$ T_{a}\frac{dv}{v} = -t \Rightarrow v = e^{-t/T_{a}} $$
Подставляем во второе уравнение: $$ T_{a}du = T_{a}e^{-t/T_{a}}Qdt $$
и находим: $$ du = Qe^{-t/T_{a}}dt \Rightarrow u = \intop_{0}^{t}e^{-t/T_{a}}dt = Q(e^{t/T_{a}}-1) $$
Таким образом, искомая функция выручки: $$ r = uv = Qe^{-t/T_{a}}(e^{t/T_{a}}-1) = Q(1-e^{-t/T_{a}}) $$
Конечно можно было пойти менее трудоемким путем и воспользоваться автоматическим решателем дифференциальных уравнений или найти численное решение, впрочем численное решение не позволит использовать параметры полученного уравнения для моделирования прогнозной выручки.
Как уже упоминалось, рассмотренная функциональная зависимость достаточно универсальна и может быть использована для прогнозирования в различных областях в т.ч. на финансовых рынках, например, при построении кривой доходности для облигаций.
Параметры функции модельной выручки
Следующим логичным шагом будет – поиск конкретных параметров функции, а именно (T_{a}) и (Q), для чего можно использовать Ньютоновский
алгоритм и функцию nls() в R. Кроме того, усложним задачу алгоритму и
не станем задавать конкретного значения мощности барбершопа. Пусть алгоритм подберет этот параметр автоматически:
# Ищем значения сразу двух параметров: power и Ta
nl_fit1 <- nls(data = sim_bshop,
bshop1 ~ power*(1-exp(-day_num/Ta)), #указываем функцию
start = list(power = 100, Ta = 120)) #указываем стартовые значения параметров
# Выводим результат
nl_fit1
## Nonlinear regression model
## model: bshop1 ~ power * (1 - exp(-day_num/Ta))
## data: sim_bshop
## power Ta
## 32.5 151.9
## residual sum-of-squares: 15205
##
## Number of iterations to convergence: 4
## Achieved convergence tolerance: 8.577e-07
И для второго барбершопа:
# Ищем значения сразу двух параметров: power и Ta
nl_fit2 <- nls(data = sim_bshop,
bshop2 ~ power*(1-exp(-day_num/Ta)), #указываем функцию
start = list(power = 100, Ta = 130)) #указываем стартовые значения параметров
# Выводим результат
nl_fit2
## Nonlinear regression model
## model: bshop2 ~ power * (1 - exp(-day_num/Ta))
## data: sim_bshop
## power Ta
## 49.01 154.95
## residual sum-of-squares: 33387
##
## Number of iterations to convergence: 4
## Achieved convergence tolerance: 3.628e-07
Сравним результаты:
| Барбершоп | Теоритическая Q | Модельная Q |
|---|---|---|
| # 1 | 48 | 32.5 |
| # 2 | 72 | 49.01 |
Можно легко заметить существенное расхождение теоретических и модельных значений, что очевидно связано с недельными колебаниями спроса. Другими словами, достижение объема выручки, соответствующей теоретической мощности – это скорей удачное стечение обстоятельств нежели обыденная практика. Постоянная работа на теоретическом пределе мощности – есть несбыточная мечта любого бизнеса. Усредненное значение отклонений от теоретической мощности ~ 32.6%. Этот параметр пригодиться позже.
Требования к объему данных
Очевидно, что больший объем фактических данных всегда будет позитивно сказываться на точности прогноза, но сколько данных в действительности нужно для того чтобы можно было доверять прогнозу? Открывается новый барбершоп и очень хочется поскорее узнать сколько же денег этот барбершоп будет приносить. 👀
# функция оценки параметра Ta (для нового барбершопа 3), которая на вход принимает изменяемый интервал времени
get_Ta_est <- function(day){
nls(data = sim_bshop[1:day,],
bshop2 ~ 6*12*(1-0.326)*(1-exp(-day_num/Ta)),
start = list(Ta = 100)) %>%
coefficients()}
get_Ta_est(15) # проверка работы функции на 15 день открытия
## Ta
## 89.44865
need_day <- 5:100 %>% # пробегаемся циклом по интервалу от 5 дней до 100 дней
map_dfr(~get_Ta_est(.), .id = "need_day")
# Строим график и делаем заключения, значимые для бизнеса
need_day %>%
mutate(need_day = as.numeric(need_day)) %>%
ggplot() +
annotate("text_npc", npcx = .5, npcy = .5, label = "InvestCookies.ru", color = "#1D1E20", alpha = .9, size = 20) +
geom_line(aes(x = need_day, y = Ta), col = my_pal[1], size = 1) +
geom_hline(yintercept = Ta, col = my_pal[2], linetype = 5, size = 1) +
annotate(x = 50, y = 180, geom = "text", label = "Истинный уровень\nразгонной динамики\nTa = 150", col = my_pal[2], vjust = .5, hjust = 0, size = 6) +
geom_curve(aes(x = 50, y = 180, xend = 30, yend = 150), arrow = arrow(length = unit(0.03, "npc")), col = my_pal[2], size = 0.5) +
labs(title = "График стабилизации параметра Та\nв зависимости от размера интервала оценки модели", x = "Размер интервала") +
ylim(70, 200)

Уже примерно с 25 дня модель становится достаточно уверенной 👍👍👍 для того чтобы прогнозам можно было доверять. Поэтому уже на 25 день старта нового барбершопа можно корректировать коммерческие и финансовые планы на 2 года вперед исходя из более точного прогноза. Уже неплохо 😎.
Доверительные интервалы
Очень часто доверительные интервалы являются более важными чем непосредственно прогнозные значения искомого показателя. С точки зрения менеджмента необходимо понимать какой уровень запасов формировать для того чтобы не было кассовых разрывов или простоев из-за нехватки ресурсов. С другой стороны, слишком большие запасы ведут к неэффективному использованию денежных средств хотя бы потому, что существует инфляция и какая-то внутренняя норма доходности для бизнеса. Как говорится: “Деньги стоят денег.” Поэтому хороший финансовый директор будет рачительно относится к необходимому объему остатков на счетах. Оценка доверительных интервалов позволяют дальновидному менеджменту пройти между этими своеобразными Сциллой и Харибдой т.е. не держать слишком большие запасы с одной стороны и не повышать риск кассовых разрывов – с другой.
Полученное ранее решение дифференциального уравнения не является линейным. Нелинейные модели в отличие от линейных не могут использовать методы классической статистики для оценки доверительных интервалов поэтому в данном случае используется техника bootstrap. Суть этой техники заключается в многократном извлечение части данных из располагаемой выборки с дальнейшей оценкой параметров модели для каждой извлеченной части данных, после чего можно сделать оценку насколько сильны отклонения от модельной (прогнозной) кривой путем простого усреднения.
sim_bshop_btstrp1 <- sim_bshop %>%
select(day_num, bshop3) %>% # выбираем барбершоп 3 (для остальных линий используется аналогичный прием)
slice(1:25) %>% #выбираем первые 25 дней в качестве отрезка для прогнозирования
bootstraps(times = 1e3, apparent = TRUE) #семплируем (извлекаем примеры) 1000 значений из имеющейся выборки
sim_bshop_btstrp2 <- sim_bshop %>%
select(day_num, bshop3) %>% # выбираем барбершоп 3 (для остальных линий используется аналогичный прием)
slice(1:50) %>% #выбираем первые 50 дней в качестве отрезка для прогнозирования для сравнения
bootstraps(times = 1e3, apparent = TRUE) #семплируем (извлекаем примеры) 1000 значений из имеющейся выборки
# Создаем "конвеерную" функцию прогнозирования на вход которой будем подавать наши семплы
fit_nls_on_bootstrap <- function(split) {
nls(bshop3 ~ 9*12*(1-0.326)*(1-exp(-day_num/Ta)), analysis(split), start = list(Ta = 100))}
# Используем конструкцию "mutate - map" для применения "конвеерной" функции к каждому семплу
sim_bshop_mdls1 <- sim_bshop_btstrp1 %>%
mutate(model = map(splits, fit_nls_on_bootstrap),
coef_info = map(model, tidy)) # выгружаем результат оценки модели
# Используем конструкцию "mutate - map" для применения "конвеерной" функции к каждому семплу
sim_bshop_mdls2 <- sim_bshop_btstrp2 %>%
mutate(model = map(splits, fit_nls_on_bootstrap),
coef_info = map(model, tidy)) #выгружаем результат оценки модели
# Вычисляем доверительные интервалы для 25 дней
percentile_intervals1 <- int_pctl(sim_bshop_mdls1, coef_info)
# Вычисляем доверительные интервалы для 50 дней
percentile_intervals2 <- int_pctl(sim_bshop_mdls2, coef_info)
bind_rows(percentile_intervals1, percentile_intervals2) %>%
mutate(samples = c(25, 50)) %>%
select(samples, .lower, .estimate, .upper) %>%
mutate(across(-1, ~round(., 2))) %>%
datatable(style = 'bootstrap4', extensions = 'Responsive', options = list(pageLength = 10),
caption = "Доверительные интервалы для двух выборок (25 и 50 дней)")
Очевидно, что для малого количества наблюдений (25 дней) доверительные интервалы больше чем для большего количества (50 дней). Далее для прогнозирования будут использованы параметры (T_{a}=146) и (Q=170)
sim_bshop_mdls <- sim_bshop_mdls1 %>%
unnest(coef_info) %>% #упрощаем структуру результата
mutate(n = "n_25") %>% #добавляем маркер интервала
bind_rows(sim_bshop_mdls2 %>% #соединяем два примера с разными размерами интервалов (25 и 50)
unnest(coef_info) %>% #упрощаем структуру результата
mutate(n = "n_50")) #добавляем маркер интервала
# Строим графики и анализируем
sim_bshop_mdls %>%
ggplot(aes(x = estimate)) +
annotate("text_npc", npcx = .5, npcy = .5, label = "InvestCookies.ru", color = "#1D1E20", alpha = .9, size = 10) +
annotate(geom = "rect", ymin = 0, ymax = Inf, alpha = .3, fill = my_pal[1],
xmin = percentile_intervals1$.lower, xmax = percentile_intervals1$.upper) +
annotate(geom = "rect", ymin = 0, ymax = Inf, alpha = .5, fill = my_pal[1],
xmin = percentile_intervals2$.lower, xmax = percentile_intervals2$.upper) +
geom_histogram(binwidth = 5, alpha = .8) +
geom_density(aes(y = after_stat(count*5)), fill = my_pal[2], col = my_pal[2], alpha = .3) +
facet_grid(~n) +
labs(title = "Распределение оценки доверительных интервалов\nдля двух выборок с разными размерами интервалов (25 и 50 дней)",
x = "Оценка параметра Ta", y = "Количество наблюдений")
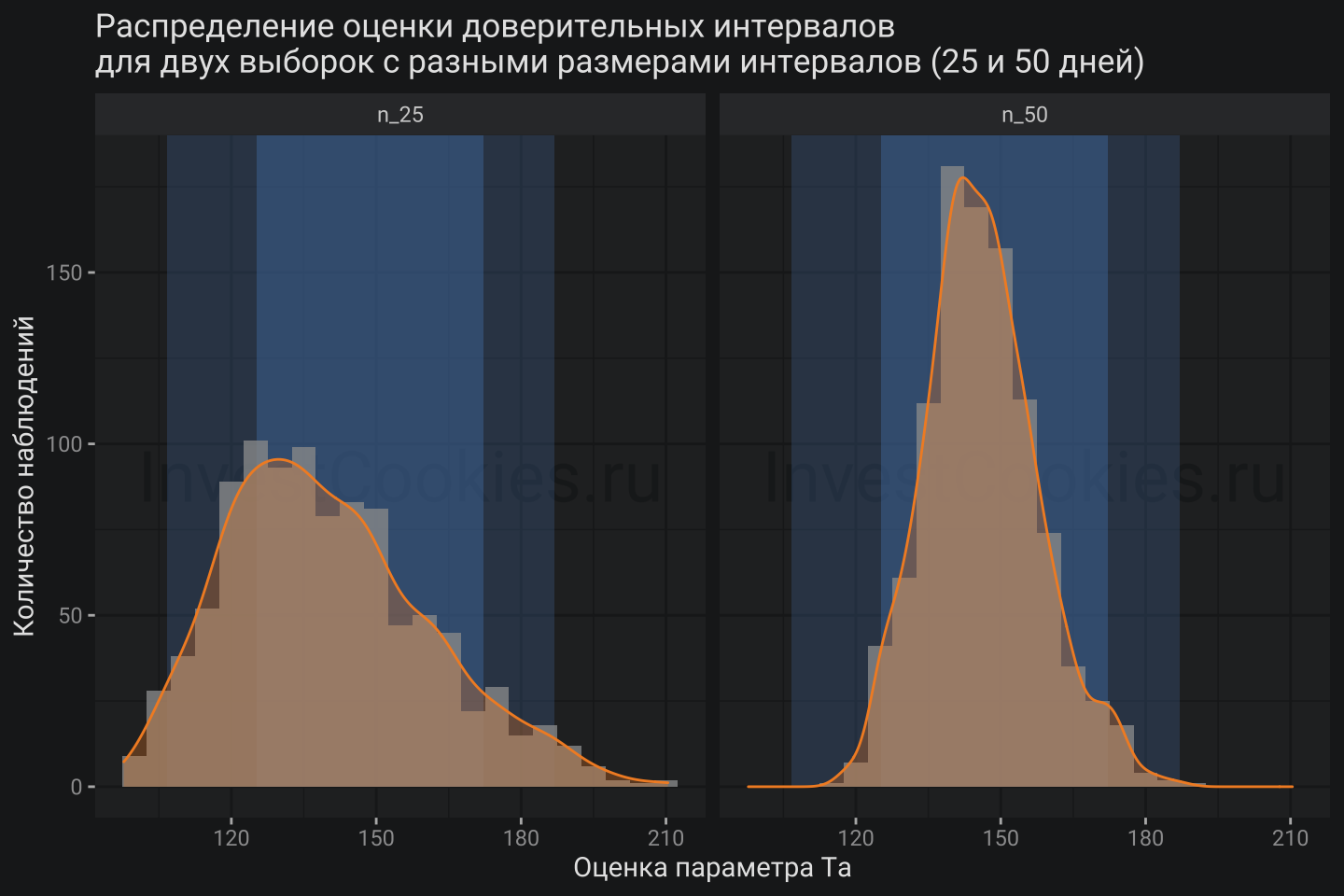
Фактически мы построили тысячи модельных кривых, которые описывают меру неопределенности разработанной модели.
# Cделаем преобразования для еще одного графика
boot_aug <- sim_bshop_mdls %>%
mutate(augmented = map(model, augment)) %>% #создаем набор данных для отображения на графике
unnest(augmented)
boot_aug %>%
ggplot(aes(x = day_num, y = bshop3)) +
annotate("text_npc", npcx = .5, npcy = .5, label = "InvestCookies.ru", color = "#1D1E20", alpha = .9, size = 10) +
geom_line(aes(y = .fitted, group = id), alpha = .05, col = my_pal[1], size = 2) +
geom_line(col = my_pal[2], size = 1, alpha = .6) +
geom_point(col = my_pal[2], size = 3, alpha = .6) +
facet_grid(~n) +
labs(title = "Сопоставление фактических данных и множественных bootstrap оценок\nдля двух выборок с разными размерами интервалов (25 и 50 дней)",
x = "Дни", y = "Выручка")
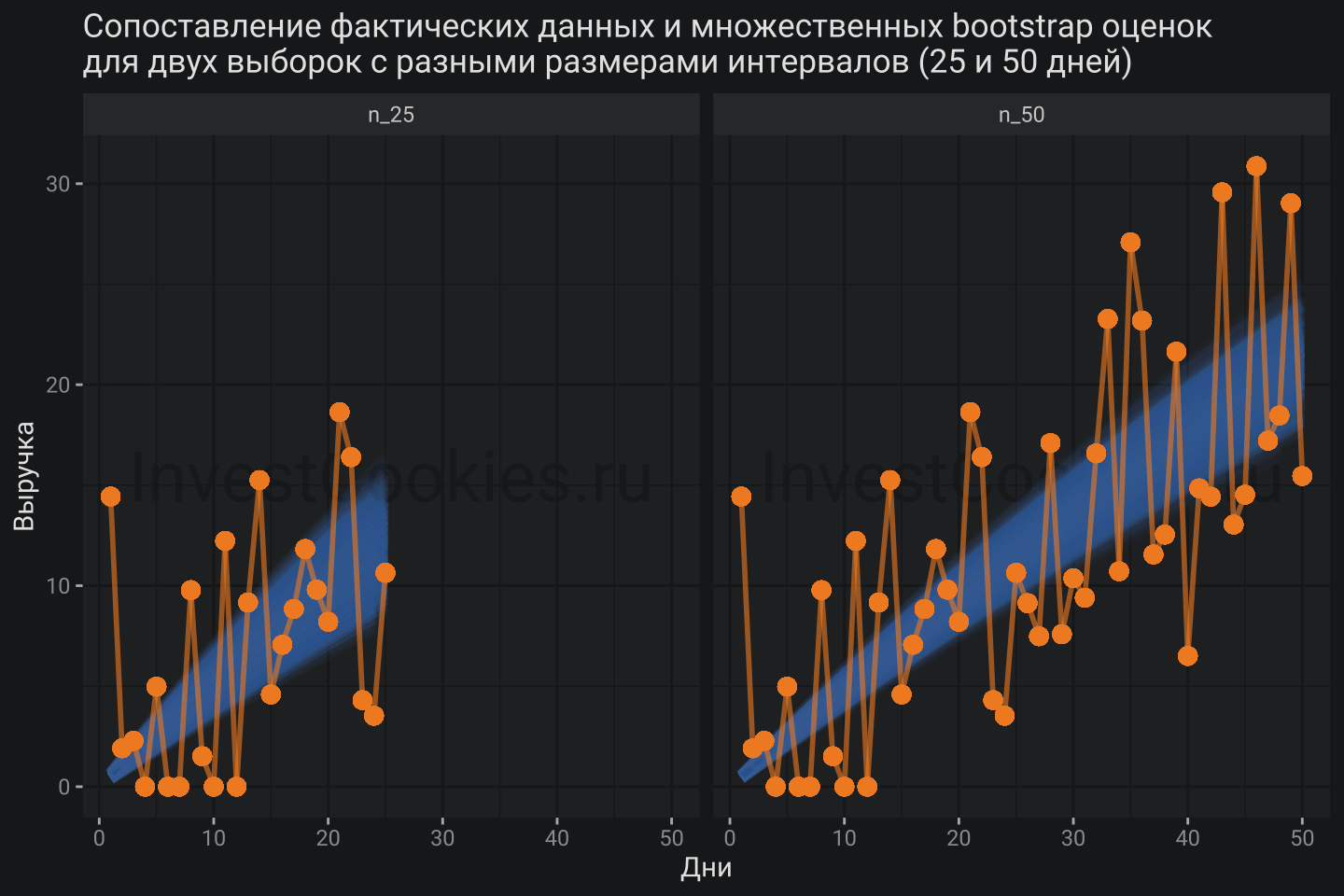
Решение реальной задачи идентификации модели кроме проделанных манипуляций еще бы требовала определение регрессионных коэффициентов, характеризующих недельный паттерн. Оставим эту задачу за рамками данной заметки и воспользуемся значениями коэффициентов, которые были определены на этапе генерации данных. Для того чтобы доверительные интервалы не выглядели как пила по каждой недели наблюдений были отобраны лишь максимальные и минимальные значения, которые использовались в качестве верхнего и нижнего уровней доверительных интервалов. Такой трюк исполняется лишь для того чтобы график доверительных интервалов выглядел красиво 😻, а почему бы собственно нет? Получаем следующую картинку прогноза:
sim_bshop %>%
rownames_to_column("index") %>%
mutate(index = as.numeric(index),
bshop_mdl = 12*9*(1-exp(-index/146))*week_effect,
bshop_mdl_up = 12*9*(1-exp(-index/124.56))*week_effect,
bshop_mdl_low = 12*9*(1-exp(-index/168.21))*week_effect) %>%
group_by(week_n) %>%
mutate(bshop_mdl_up = max(bshop_mdl_up), bshop_mdl_low = min(bshop_mdl_low)) %>%
ungroup() %>%
e_charts(day_num) %>%
e_line(bshop3, itemStyle = list(borderColor = NULL, opacity = .5),
lineStyle = list(opacity = .5), color = my_pal[1], name = "Барбер 3") %>%
e_line(bshop_mdl, itemStyle = list(borderColor = NULL, opacity = .5),
lineStyle = list(opacity = .5), color = my_pal[2], name = "Модель") %>%
e_band(bshop_mdl_low, bshop_mdl_up, areaStyle = list(list(color = 'none'), list(color = my_pal[2], opacity = .2))) %>%
e_mark_line(serie = "Барбер 3", title = "Начало прогноза", data = list(xAxis = 50), label = list(color = my_pal[1])) %>%
e_datazoom(x_index = 0, type = "slider") %>%
e_tooltip(trigger = "axis", digits = 0, textStyle = list(color = "white"), axisPointer = list(type = "line"),
formatter = htmlwidgets::JS("function (param) {
let param1 = param[1];
let param2 = param[0];
return [
'<b>День</b>: ' + param1.value[0] + '<hr size=1>',
'<b>Барбершоп 3</b>: ' + Math.round(param1.value[1]) + ' тыс. руб.' + '<br/>',
'<b>Модель</b>: ' + Math.round(param2.value[1]) + ' тыс. руб.' + '<br/>',
].join('');}")) %>%
e_title(text = "Динамика выручки барбершопов") %>%
e_y_axis(name = "Выручка, тыс. руб.") %>%
e_x_axis(name = "День") %>%
e_legend(type = "scroll", padding = 30) %>%
e_draft("InvestCookies.ru", size = "80px", opacity = 0.4)
Выводы
Представленный подход позволил получить прогноз с учетом эмпирических знаний о динамике исследуемого процесса. Дифференциальное уравнение, которое использовалось для прогноза – является далеко не единственным. В теории автоматического управления существуют и другие динамические уравнения, каждое из которых имеет аналитическое решение. Разумно подытожить важнейшие моменты разработки параметрических моделей с использованием динамических уравнений:
- Динамическое уравнение составляется из эмпирических знаний и требует хорошего понимания предметной области
- Хорошая новость состоит в том, что в каждой предметной области зачастую уже можно найти составленные и апробированные уравнения
- Динамическое уравнение не обязательно решать аналитически, но это очень желательно для интерпретируемости модели
- Подгонка параметров модели может быть сделана с помощью алгоритмов минимизации суммы квадратов для нелинейных функций, например, методом Гаусса-Ньютона
- Параметрические модели позволяют делать состоятельные прогнозы даже при относительно небольшом количестве наблюдений благодаря тому, что модель усилена эмпирическими знаниями
- Оценка доверительных интервалов – крайне важна для принятия управленческих решений и может быть получена с помощью техники bootstrap для нелинейных моделей
- Динамические уравнения универсальны для различных предметных областей и один раз разобравшись с такой техникой – эту технику можно использоваться неоднократно
