Простые эвристики для TSP

Точные и неточные решения

В прошлой заметке я поднял тему ванильно-радужных перспектив использования искусственного интеллекта для решения оптимизационных задач, в частности, для решения хорошо изученной задачи коммивояжера, она же TSP (Travelling Salesman Problem). Там же был дан старт разбору некоторых классических алгоритмов для решения этой задачи в рамках чего я представил подход, основанный на MIP (Mixed Integer Programming). Считаю важным завершить такой разбор для лучшего понимания отличий в работе нейронных сетей.

Ранее я упоминал, что решение оптимизационных задач при более-менее серьезной размерности заставляет делать выбор между точностью и скоростью расчетов. Метод MIP играет на стороне точности и его вычислительные пределы легко прощупать запуском алгоритма не для 16 городов, как было презентовано ранее, но для 32. Лично я не смог дождаться завершения расчетов для такой размерности: что уж там говорить про вариант на 64 города. Впрочем, это не означает отсутствие в природе точных решений для крупных задач за ограниченное время. Олень с картинки-тизера красуется не только для новогоднего настроения, но сама картинка – есть ничто иное как точное решение задачи коммивояжера на 200 тысяч городов. В действительности, существует царь-алгоритм для точного решения TSP и этот алгоритм, кроме всего прочего, использует MIP подход, но сфера применимости тут – TSP и только TSP.

Неточные алгоритмы играют на стороне скорости вычислений и обычно эксплуатируют некие простые идеи, например, идею посещения ближайшего города в задаче коммивояжера. Также неточные численные методы могут быть вдохновлены аналогиями реального мира, что определяет их интригующие названия: Муравьиный алгоритм, Имитации отжига, Генетический алгоритм и пр. Преимуществом алгоритмов с собственными названиями в том, что они достаточно универсальны, то есть могут хорошо справляться с поиском глобального минимума в любой ситуации. Например, ML-фреймворк mlr3 позволяет использовать имитацию отжига для тюнинга гиперпараметров ML-моделей. Также в личной практике я успешно применял Генетический алгоритм для оптимизации количества погрузочной техники, движение которой задавалось относительно простой эвристикой.

С течением времени мое небольшое исследование превратилось в кучу слабо-организованных скриптов и нужно было как-то все переупаковать для унификации, что делает возможность запуск тестовых расчетов и сравнение алгоритмов между собой. Приятным побочным эффектом такой унификации – является возможность переиспользования некоторых функций сразу в нескольких алгоритмах. Проект расположен на github, где выложен исходный код каждого алгоритма. Поэтому далее я позволю себе пропустить второстепенные подробности и сфокусироваться на уровне значимых идей реализации. Первым шагом необходимо определить уже знакомую по первой заметке тестовую задачу:

library(ggplot2) 
# Загрузка вспомогательных функций из проекта ai_optimization, расположенного на github
"https://raw.githubusercontent.com/dkibalnikov/ai_optimization/refs/heads/main/algorithms/functions.R"|>
  source()

# Размерность задачи коммивояжера
n_cities <- 16

# Создание тестовой задачи идентичной задачи из первой заметки
cities <- generate_task()

# Вывод картинки
p0 <- as.data.frame(cities) |> 
  transform(n=seq_len(n_cities)) |>
  ggplot(aes(x, y)) + 
  geom_point() + 
  geom_point(data = data.frame(n=1, x=0, y=0), shape = 21, size = 5, col = "firebrick") +
  geom_text(aes(label = n), nudge_x = 3)

p0

Как и в подходе MIP неточные алгоритмы используют симметричную матрицу расстояний между городами, которая может быть получена с помощью базовой функции R dist():

dist_mtrx <- as.matrix(dist(cities))

# Визуализация матрицы расстояний
apply(dist_mtrx, 2, \(x)round(x,1)) |> 
  as.data.frame(dist_mtrx) |> 
  emphatic::hl(scale_color_viridis_c()) |> 
  emphatic::as_html(font_size = "11px")

         1    2    3     4     5    6     7     8    9    10    11    12    13    14    15    16
1      0.0 51.7 93.3 112.1 103.1 83.8  71.5 115.0 47.5  85.8 113.7  91.3 125.5 106.7 110.3 115.6
2     51.7  0.0 41.8  66.8  71.0 34.7  27.4  72.9 23.2  36.5  62.1  78.5  78.4  64.7  70.4  67.3
3     93.3 41.8  0.0  37.0  60.5 15.3  37.5  47.2 52.9  23.9  21.0  85.9  43.2  41.6  49.0  31.2
4    112.1 66.8 37.0   0.0  34.0 33.0  72.8  11.2 65.0  60.8  40.2  68.4  14.4  10.7  16.2  12.2
5    103.1 71.0 60.5  34.0   0.0 48.5  87.9  25.9 57.7  81.5  71.4  35.7  45.6  23.5  18.6  46.1
6     83.8 34.7 15.3  33.0  48.5  0.0  41.1  41.0 40.0  33.0  34.8  71.1  43.8  33.6  40.6  32.6
7     71.5 27.4 37.5  72.8  87.9 41.1   0.0  81.8 50.3  17.2  51.6 102.5  80.6  74.7  81.7  68.6
8    115.0 72.9 47.2  11.2  25.9 41.0  81.8   0.0 67.6  70.9  51.4  61.5  19.8   8.4   7.4  22.8
9     47.5 23.2 52.9  65.0  57.7 40.0  50.3  67.6  0.0  56.3  73.9  57.2  78.7  59.3  63.0  69.6
10    85.8 36.5 23.9  60.8  81.5 33.0  17.2  70.9 56.3   0.0  34.7 101.8  66.6  64.8  72.1  54.7
11   113.7 62.1 21.0  40.2  71.4 34.8  51.6  51.4 73.9  34.7   0.0 101.4  39.0  48.9  55.9  29.2
12    91.3 78.5 85.9  68.4  35.7 71.1 102.5  61.5 57.2 101.8 101.4   0.0  81.1  57.7  54.1  79.9
13   125.5 78.4 43.2  14.4  45.6 43.8  80.6  19.8 78.7  66.6  39.0  81.1   0.0  24.0  27.0  12.1
14   106.7 64.7 41.6  10.7  23.5 33.6  74.7   8.4 59.3  64.8  48.9  57.7  24.0   0.0   7.4  22.6
15   110.3 70.4 49.0  16.2  18.6 40.6  81.7   7.4 63.0  72.1  55.9  54.1  27.0   7.4   0.0  28.4
16   115.6 67.3 31.2  12.2  46.1 32.6  68.6  22.8 69.6  54.7  29.2  79.9  12.1  22.6  28.4   0.0

Ближайший город

Идея посещения ближайшего города реализуется очень просто:

В столбце матрицы расстояний выбирается наименьшее значение и определяется индекс строки этого значения
Выбранный индекс записывается в память и делается переход в столбец с номером этого индекса
Далее процесс повторяется аналогично, но с исключением уже посещенных городов

Кстати, вместо матрицы расстояний можно использовать какую-то другую матрицу весов, например, результат Q-learning алгоритма, который популярен для обучения в робототехнике. Собственно, использованная ниже функция get_route4mtrx() для поиска решения – есть заимствованный элемент из Q-learning решения, который хочется обсудить в другой раз.

# Решение TSP c эвристикой ближайшего соседа (города)
res_closest <- get_route4mtrx(-dist_mtrx)

# Расчет итоговой дистанции решения
sol_dist_closest <- calc_dist4mtrx(dist_mtrx, res_closest) |> round(2)

# Визуализация решения 
prep4plot(cities, res_closest) |> 
  plot_tour(F) + 
  scale_color_viridis_c(begin = .3) + 
  labs(title = paste0("Ближайший город: ", sol_dist_closest))

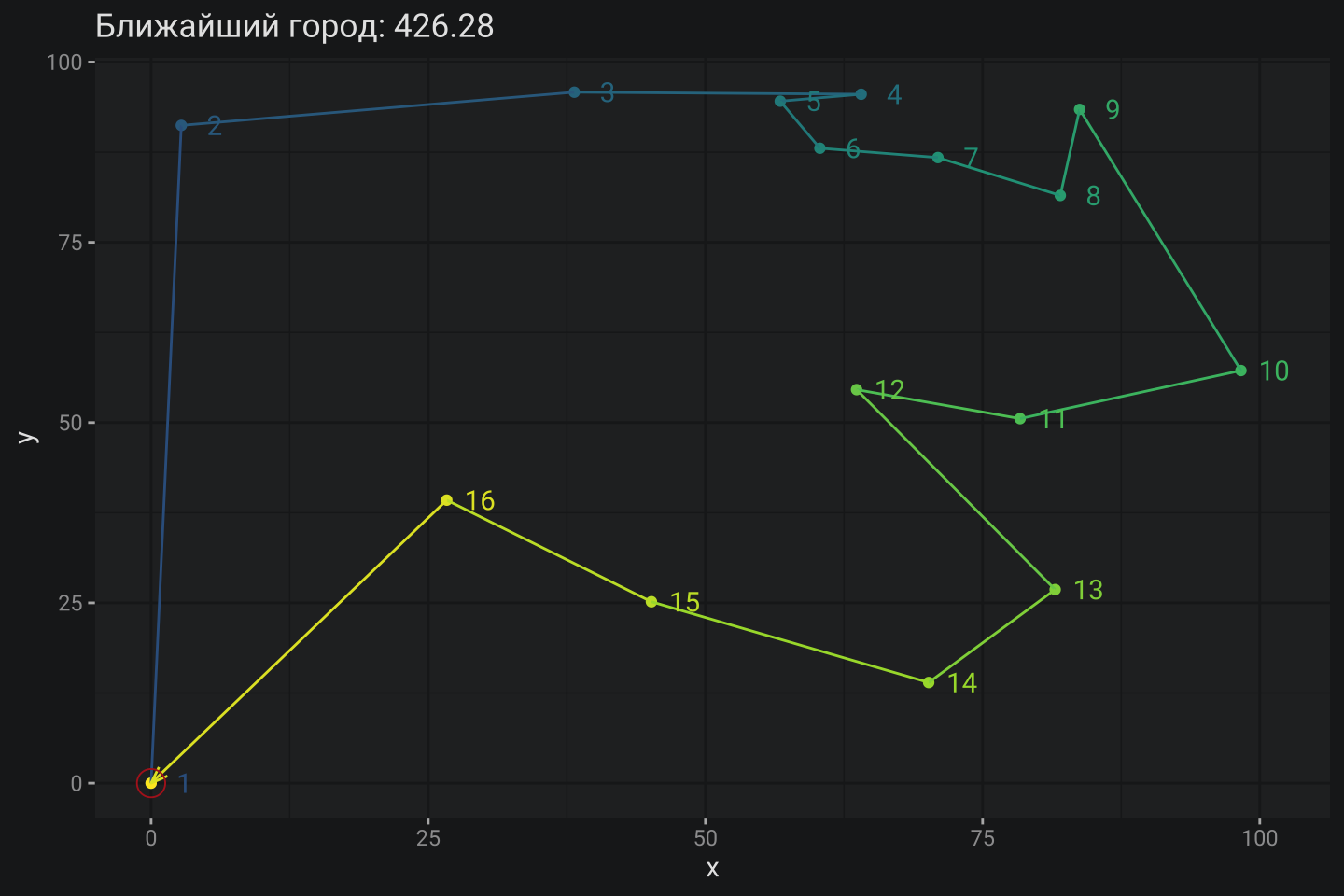
Решение по методу Ближайшего города всего на ~5% хуже оптимального. Я считаю – это очень даже неплохо, но будет ли это справедливо для более широкого круга задач? Действительно, возможно, этот метод хорошо ложится на базовую задачу, но будет давать результаты хуже на других примерах. Собственно, это и можно будет проверить на этапе тестирования для некоторой выборки примеров.

2 - opt

Далее предлагаю взять оптимальное MIP-решение текущей задачи и намеренного его испортить, переставив порядок посещения городов:

Вместо города №2 поставить город №15
Вместо города №15 поставить город №2

Очевидно, получится не очень оптимальный результат:

# Ссылка на результат точного решения MIP
link2MIP_sol <- "https://github.com/dkibalnikov/ai_optimization/raw/refs/heads/main/test_results/MIP_16nodes.rds"
dest_dir <- tempfile(fileext = ".rds") # путь и имя для временного файла

download.file(link2MIP_sol, dest_dir) # загрузка решение
MIP_sol16 <- readRDS(dest_dir) # чтение 

example_route <- dplyr::filter(MIP_sol16, seed ==2021)[["route"]][[1]] # выбор целевого примера
swap_route <- example_route # создание нового не оптимального варианта 
swap_route[2] <- example_route[15] # замена города 15 --> 2
swap_route[15] <- example_route[2] # замена города 2 --> 15

# Расчет итогового пути
swap_dist <- calc_dist4mtrx(dist_mtrx, swap_route) |> round(2)

# Визуализация не оптимального решения
generate_task() |>
  prep4plot(swap_route) |>
  plot_tour(F) + 
  geom_line(data = cities[swap_route[2:3], ], aes(x, y), col = "black", lty = 3, linewidth=1) + 
  geom_line(data = cities[swap_route[14:15], ], aes(x, y), col = "black", lty = 3, linewidth=1) +
  geom_line(data = cities[example_route[2:3], ], aes(x, y), col = "firebrick", lty = 3, linewidth=1) + 
  geom_line(data = cities[example_route[14:15], ], aes(x, y), col = "firebrick", lty = 3, linewidth=1) +
  scale_color_viridis_c(begin = .3) + 
  labs(title = paste0("Пример неоптимальности решения с перепутанными городами: ", swap_dist))

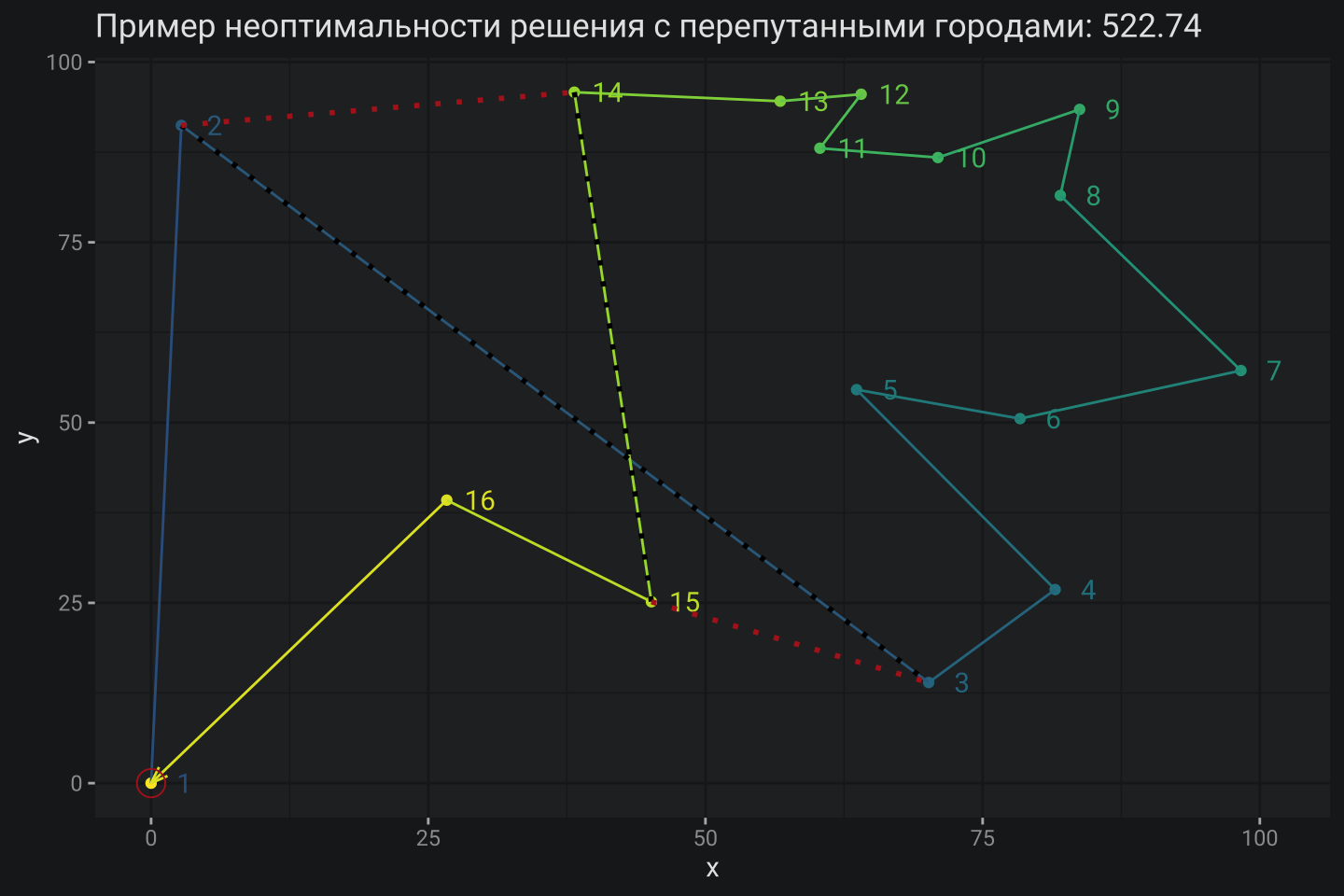
Также очевидно, что обратная своп-операция (что-то вроде переподключения концов отрезка) вернет решению его оптимальность. Идея алгоритма 2-opt состоит в том чтобы последовательно производить такие своп-операции пока решение не достигнет лучшего варианта без гарантий оптимальности. Для реализации метода потребуется две вспомогательные функции:

# Функция генерации случайного маршрута
random_route <- function(cities){
  n_cities <- seq_len(nrow(cities)) # определение размерности задачи
  route <- sample(n_cities[-1]) # случайная перестановка городов за исключением первого
  route <- c(1, route,1) # возвращаемся в исходный город
  return(route)
}
rand_route <- random_route(cities)
cat("Случайны маршрут: ", rand_route, "\n")

## Случайны маршрут:  1 6 7 3 4 5 16 15 11 2 10 14 13 12 9 8 1

# Функция своп-операции (первая позиция должна иметь индекс меньше второй)
swap <- function(route, i, k){
  c(route[1:(i-1)], route[k:i], route[(k+1):length(route)] )
}

cat("Случайны маршрут после своп-операции: ", swap(rand_route, 2, 8))

## Случайны маршрут после своп-операции:  1 15 16 5 4 3 7 6 11 2 10 14 13 12 9 8 1

Принципиальное описание алгоритма:

Старт со случайного маршрута
Запускается цикл поиска решения до момента пока решение перестает улучшаться
Запускается внешний цикл итераций по городам
Запускается внутренний цикл итераций по городам: внешний и внутренний цикл образуют пару городов для своп-операции
Осуществление своп-операции и расчет дистанции нового маршрута
Сохранение результата, если найдено что-то лучшее и выход из внешнего, внутреннего циклов
Продолжение работы цикла поиска решения согласно пункту №2 до наступления условия остановки

#  Функция для 2-opt оптимизации
two_opt <- function(cities, dist_mtrx){
  
  # Старт алгоритма - случайный маршрут
  best_route <- random_route(cities) 
  # Дистанция стартового маршрута
  min_d <- calc_dist4mtrx(dist_mtrx, best_route)  
  
  # Переменная для отслеживания найденных решений
  track_dist <- c()
  
  while(T){ # запуск цикла своп-операций до наступления условия завершения break
    old_d <- min_d # сохранение текущей дистанции до итерирования по i и k
    break_loop <- F # переменная условия остановки цикла
    for(i in 2:(nrow(cities)-1)) { # внешний цикл итерирования по городам
      for(k in (i+1):nrow(cities)) { # внутренний цикл итерирования по городам 
        # Осуществление своп-операции
        route <- swap(best_route, i, k) # новое решение
        new_d <- calc_dist4mtrx(dist_mtrx, route) # новая дистанция 
        
        # Сохранение решения 
        if(new_d < min_d){ # если решение лучше то оно сохраняется
          min_d <- new_d
          best_route <- route
          break_loop <- T
          break() # остановка внутреннего цикла, если найдено решение лучше
        }
      } 
      if(break_loop) break() # выход из внешнего цикла
    } 
    if(old_d == min_d) break() # проверка, если внешний цикл смог получить лучшее решение
    track_dist <- c(track_dist, new_d) # сохранение решения в переменную отслеживания
  } 
  list(distance = min_d, route = best_route, track_dist = track_dist)
}

# Непосредственно расчет 
system.time(res_two_opt <- two_opt(cities, dist_mtrx))

##    user  system elapsed 
##   0.040   0.001   0.041

# Визуализация
prep4plot(cities, res_two_opt$route[-length(res_two_opt$route)]) |> 
  plot_tour() + 
  scale_color_viridis_c(begin = .3) + 
  labs(title = paste0("2-opt решение: ", round(res_two_opt$distance, 2)), 
         caption = "Исходный порядок задачи обозначен кирпичным цветом") + 
  theme(plot.caption = element_text(color = "firebrick"))

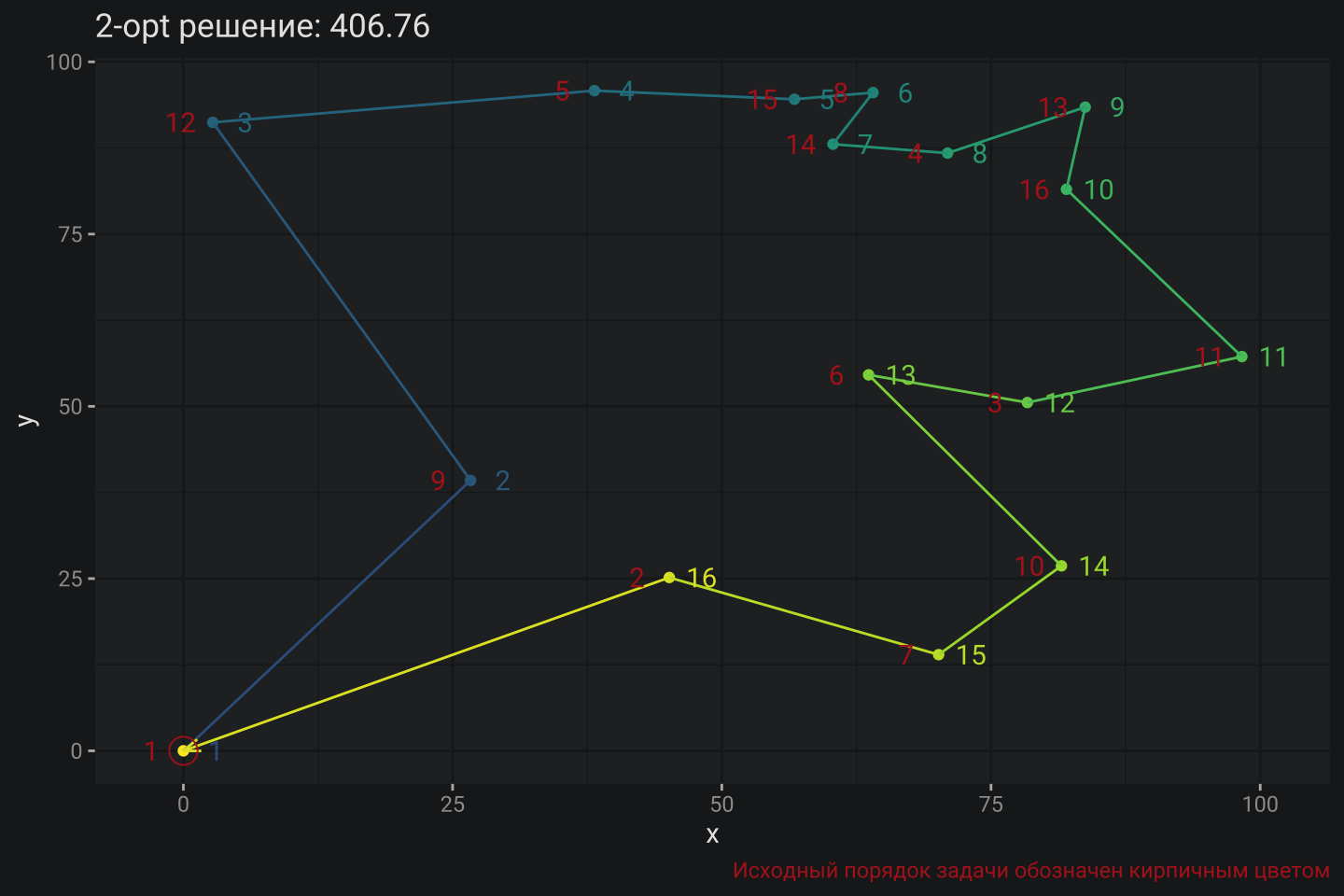
В данном случае 2-opt нашел оптимальное решение, но это не гарантированный результат. Действительно, 2-opt может легко свалиться в локальный минимум так как по факту делается всего одна своп-операция за оптимизационный проход. Именно поэтому алгоритм относится к классу поиска локального оптимума, но не глобального.

Имитация отжига (Simulated annealing)

В продолжение темы недостатков 2-opt можно закономерно желать получение модификации алгоритма, способной к поиску глобального минимума. Идея состоит в том, чтобы реализовать надстройку над 2-opt в виде стохастического эффекта, способного выталкивать решение с ямы локального минимума. Естественно, будет странным, если сила(энергия) таких толчков останется постоянной так как в этом случае решение будет мотать по пространству оптимизации, не давая шансов обнаружить локальный минимум. Не стоит забывать, что поиск локального минимума отрабатывает слишком хорошо чтобы отказаться от него полностью. Таким образом, интересно снижать энергию таких толчков из ямы по какому-то закону, например, по физическому закону кристаллизации вещества. Пусть [\Delta] – это разница дистанций решений до своп-операции и после. Тогда можно записать вероятность принятия альтернативного состояния, то есть состояния после своп-операции, следующим образом: [\rho=e^{\Delta/t}], где [t] – это температура, которая уменьшается с каждой итерацией алгоритма. В итоге большее преимущество своп-операции повышает шанс перехода в новое состояния, но с течением времени при уменьшении температуры вероятность таких переходов снижается.

# temp - стартовая температура 
# cooling - скорость "остывания"
# break_after - отсечка для остановки 
sim_anneal <- function(cities, dist_mtrx, temp=1e4, cooling=1e-3, break_after=2e2){
  # Старт алгоритма - случайный маршрут
  best_route <- random_route(cities)
  min_d <- calc_dist4mtrx(dist_mtrx, best_route)
  
  # Переменные для отслеживания 
  track_temp <- NULL # температура
  track_prob <- NULL # вероятность перехода
  track_dist <- NULL # дистанция
  
  stable_count <- 0 # счетчик отсутствия улучшений
  # Запуск цикла своп-операций до наступления условия завершения break_after
  while(stable_count < break_after){ 
    # Выбор случайной пары индексов для своп-операции 
    # с соблюдением необходимого порядка для swap()
    ik <- sort(sample(2:nrow(cities), 2))
    # Осуществление своп-операции
    new_route <- swap(best_route, i=ik[1], k=ik[2]) # новый кандидат маршрута
    new_d <- calc_dist4mtrx(dist_mtrx, new_route) # дистанция нового кандидата
    
    # Расчет преимущества текущего маршрута и кандидата
    delta <- min_d - new_d 
    # Расчет вероятности одобрения кандидата по формуле отжига
    p_adjust <- ifelse(delta > 0, 1, exp(delta/temp)) 
    # Решение об одобрении кандидата
    adjust <- ifelse(p_adjust >= runif(1,0,1), T, F)
    
    if(adjust) { # если кандидат одобрен
      best_route <- new_route # сохранение кандидата в переменную текущего/лучшего состояния
      min_d <- new_d # сохранение дистанции кандидата 
      stable_count <- 0 # обновления счетчика отсутствия улучшений
    } else {stable_count <- stable_count+1}
    # сохранение промежуточных параметров модели в переменные отслеживания
    track_temp <- c(track_temp, temp)
    track_prob <- c(track_prob, p_adjust)
    track_dist <- c(track_dist, new_d)
    # Охлаждение модели/снижения параметра темеператцры
    temp <- temp*(1-cooling)
  } # остановка цикла оптимизации
  list(distance = min_d, route = best_route, track_temp = track_temp, 
       track_prob = track_prob, track_dist = track_dist)
}

# Непосредственно расчет 
system.time(res_sim_ann <- sim_anneal(cities, dist_mtrx))

##    user  system elapsed 
##   0.881   0.109   0.992

# Визуализация
prep4plot(cities, res_sim_ann$route[-length(res_sim_ann$route)]) |> 
  plot_tour() + 
  scale_color_viridis_c(begin = .3) + 
  labs(title = paste0("Имитация отжига, решение: ", round(res_sim_ann$distance, 2)), 
         caption = "Исходный порядок задачи обозначен кирпичным цветом") + 
  theme(plot.caption = element_text(color = "firebrick"))

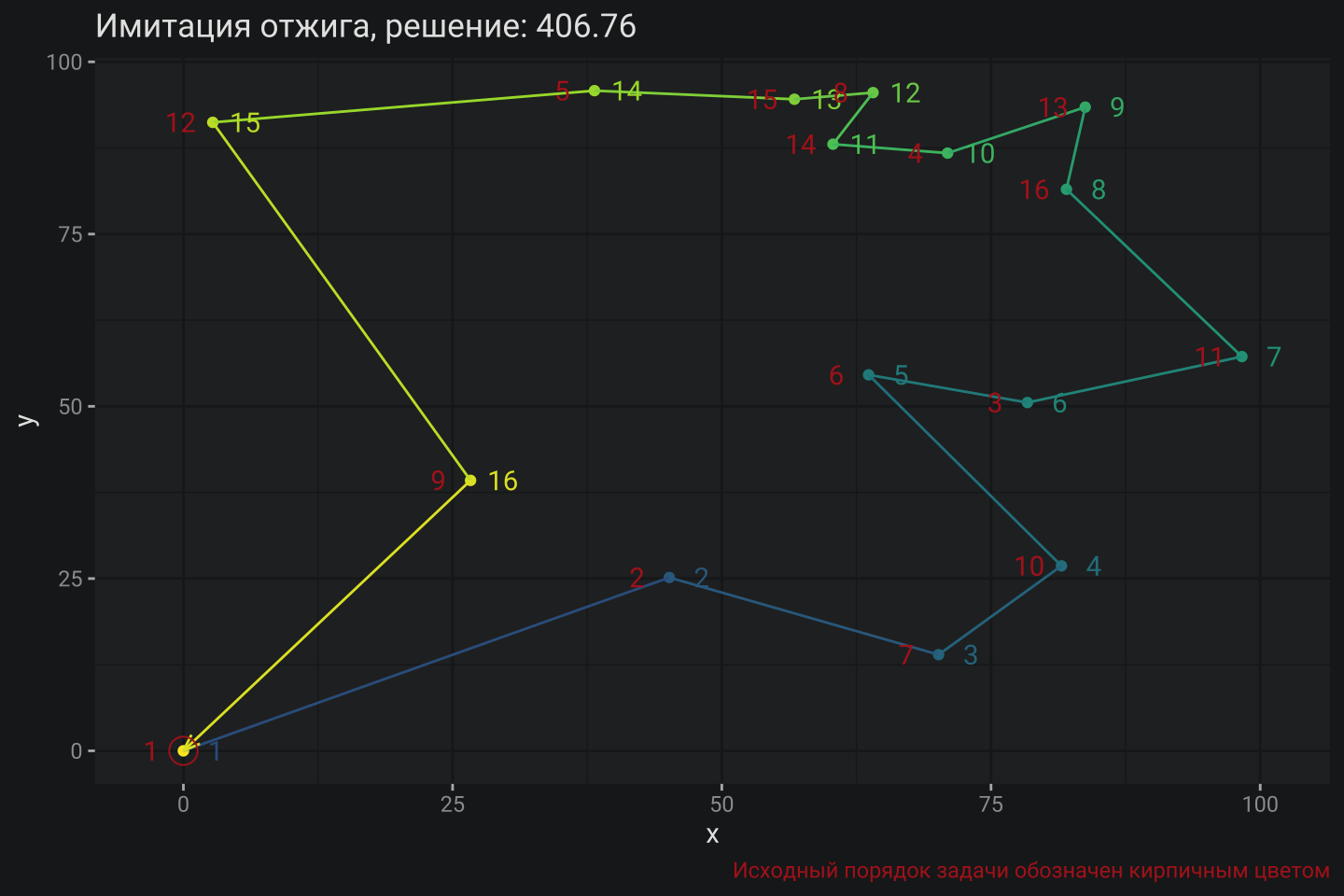
Алгоритм Имитации отжига завершил расчет базового примера тоже оптимальным решением. Осталось понять насколько этот результат будет систематически повторятся для других задач и/или других запусков расчета на базовой задаче.

Concorde

Теперь, когда на руках есть несколько велосипедных алгоритмов, можно устраивать сравнительные соревнования уездное-сельского значения. Впрочем, пожалуй, дополним группу любителей профессиональным участником. Как я упоминал в начале статьи есть некий царь-алгоритм для TSP, который находится вне конкуренции. Concorde умеет решать TSP в симметричном и несимметричном виде т.е. для центра Санкт-Петербурга с кучей односторонних дорог – он тоже подходит. Тем не менее, Concorde имеет ряд недостатков:

Алгоритм никто не менял с 2003 года. Само по себе – это лишь говорит о том, что идеал достигнут и не требует изменений. Проблема в том, что мой рабочий ноутбук Mac M1 для запуска Concorde должен скомпилировать исходники, но даже не в этом проблема. Дело в том, что стандарты компиляции C++ в новой версии Xcode другие, поэтому попытки компиляции исходников Concorde на современном окружении для Mac превращается в пытки. В общем, расчеты с помощью Concorde я делал из под Linux в облаке на маломощной машине;
Алгоритм не может быть использован для коммерческих целей, но его можно использовать для академических. Впрочем, всегда можно написать автору алгоритма и узнать его мнение по поводу использования Concorde в коммерческом ключе.

Итоговый заезд

Если речь пошла о соревнованиях, то даже для уездное-сельского формата нужен какой-то хотя бы самый простой регламент или применительно к сравнению алгоритмов – методика. Не претендуя на академическую скрупулезность, я просто сгенерировал 10 случайных задач для размерности 16, 32, 64 городов. Для каждой задачи из 10 я запускал 10 проходов алгоритма, если алгоритм имеет стохастическую природу. Concorde, MIP и алгоритм Ближайшего города запускались один раз для тестового примера. На выходе сравнивается дистанция решения и время работы алгоритма.

Исходный код расчетов, ровно как результаты лежат на github

# Загрузка предварительно скаченных с github расчетов 
tsts <- list.files("test_results", full.names = T) |> 
  lapply(readRDS) |> 
  purrr::list_rbind()

# Визуализация 
dplyr::mutate(tsts, task_size=lapply(route, \(x)ifelse(length(x)%%2==0, length(x), length(x)-1))|>unlist()) |> 
  ggplot(aes(stringr::str_wrap(model, 8), distance, fill = model, col= model)) + 
  geom_violin(alpha = .2) + 
  geom_jitter(alpha = .5) +
  facet_grid(~task_size, scales = "free") + 
  coord_flip() + 
  theme(legend.position = "none") + 
  labs(title = "Сравнение алгоритмов для задач TSP", subtitle = "Размерности: 16, 32, 64 города", 
       x = "Алгоритм", y="Дистанция итогового решения")

Формально, этот тип диаграмм называется скрипичной (violin), но в моем случае почему-то всегда получаются горшки, поэтому далее я так их и буду называть. Первое, что нужно отметить – горшок MIP решения идентичен горшку Concorde, что означает найденные двумя алгоритмами 10 оптимальных решений для 10 случайно сгенерированных задач. Во-вторых, первенство Concorde видно невооруженным глазом для всех размерностей. Метод ближайшего города почти всегда дает худший результат, за исключением размерности 64, где алгоритм Имитации отжига выглядит сопоставимо. Горшки от 2-opt в этом соревновании выглядят неплохо даже на фоне фирменных горшков от Concorde.

# Визуализация 
dplyr::mutate(tsts, task_size=lapply(route, \(x)ifelse(length(x)%%2==0, length(x), length(x)-1))|>unlist()) |> 
  ggplot(aes(stringr::str_wrap(model, 8), log(as.numeric(duration)), fill = model, col= model)) + 
  geom_violin(alpha = .2) + 
  geom_jitter(alpha = .5) +
  facet_grid(~task_size, scales = "free") + 
  coord_flip() + 
  theme(legend.position = "none") + 
  labs(title = "Сравнение алгоритмов для задач TSP", subtitle = "Размерности: 16, 32, 64 города", 
       x = "Алгоритм", y="Логарифм времени поиска решения")

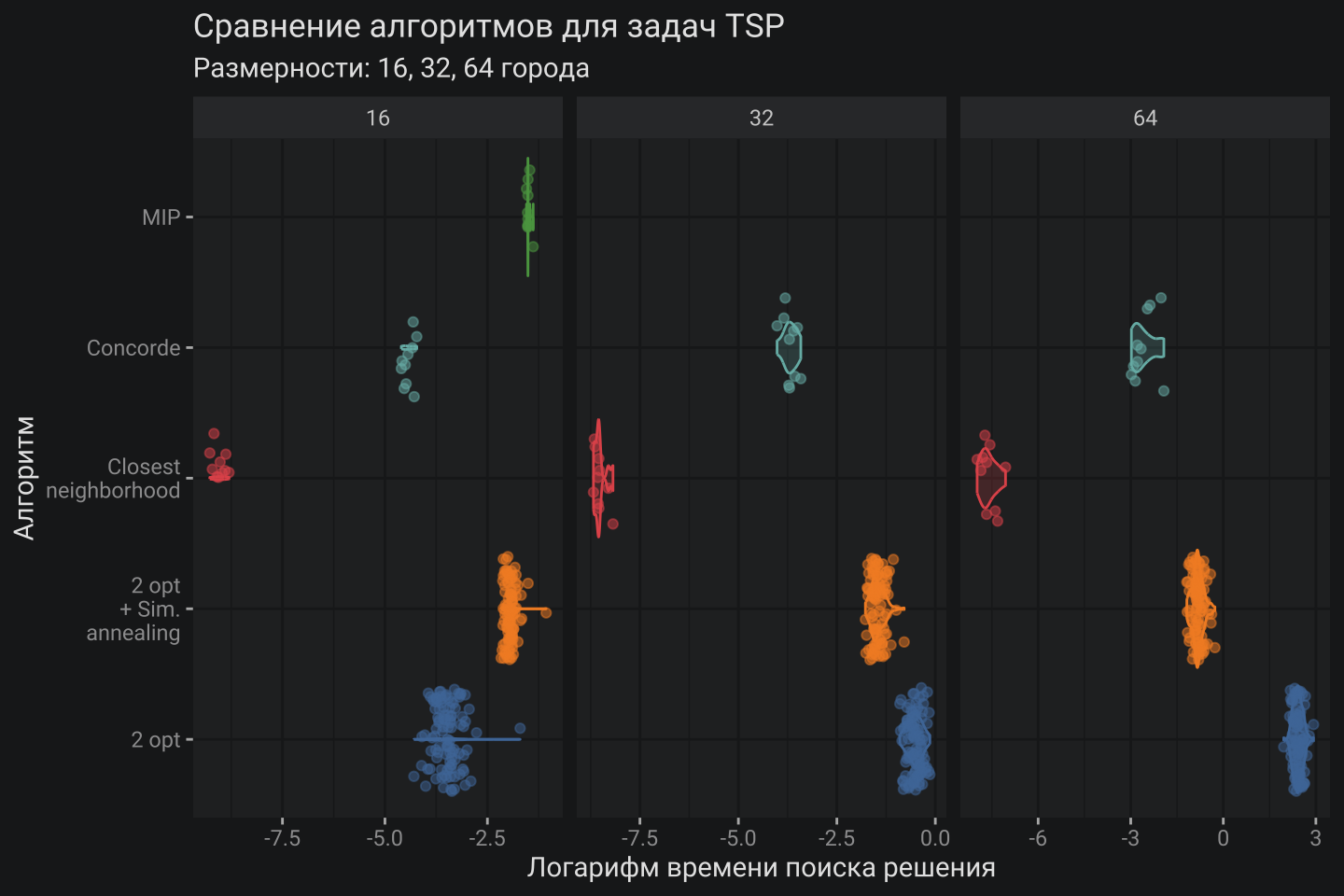
По времени поиска оптимального решения все оказалось в рамках ожиданий. MIP показывает худший результат для размерности 16 городов, а уже на 32 городах сходит с дистанции. Алгоритм Ближайшего города показывает лучшие результаты. Горшки от Concorde идут следом. Алгоритм 2-opt проигрывает Имитации отжига на размерностях более высокого порядка, то есть имеет место размен точности на время. Напомню, алгоритм Имитации отжига позволяет настраивать параметры температуры и отсечки остановки, что влияет одновременно на оптимальность решения и время расчета, делая его более гибким чем 2-opt для решения реальных боевых задач.

Источники, использованные при подготовке заметки:

Простой способ узнать о новых публикациях – подписаться на Telegram-канал:

🍪🍪🪙 InvestCookies

Точные и неточные решения#

Ближайший город#

2 - opt#

Имитация отжига (Simulated annealing)#

Concorde#

Итоговый заезд#