Где инвест печеньки? 🍪
Так случается, что иногда мне звонят ребята из чатов и упрекают меня в обмане их ожиданий. Мол, я пишу всякие умные штуки и вангую кризисы, а вот конкретно сказать когда купить и когда продать не могу. Конечно, можно было бы ответить в духе цитаты одного футболиста: ваши ожидания - ваши проблемы, но все-таки изначально я планировал писать про инвест печеньки т.е. про всякие помогалки людям, которые занимаются инвестициями. К сожалению, в определенный момент чреда известных событий перепрошила серое вещество в моей голове, которое какое-то время буквально отказывалось размышлять об инвестиционных стратегиях.
Но прошло время, индекс Мосбиржи сначала сильно просел потом частично восстановился, позволив заработать наиболее дальновидным. Были конечно и те, кто звонко щелкал сфинктером орехи от происходящего и фиксировал эпические убытки. Не уверен, что я был особенно дальновиден, но совершенно точно я остался в плюсе, стоически удерживая свои позиции на фоне эмоциональных потрясений. Отчасти это было связано с тем, что я всегда отдавал предпочтение фундаментальному анализу, но не техническому. Отдавать предпочтение – это еще не значит пользоваться исключительно одним. В целом, по прошествии некоторого времени я пришел к практике совместного использования фундаментального и технического подходов к анализу. Выглядит это приблизительно так: я перебираю инвестиционные идеи, которые подкидываются с разных сторон и выбираю для себя интересные бумаги, далее я еще точку входа с помощью относительно простой модели MACD (moving average convergence/divergence) и покупаю. При достижении приблизительных фундаментальных ориентиров роста я начинаю искать точку для продажи также с помощью MACD. Собственно по поводу MACD я и хочу поговорить поподробнее.
Использование MACD не является чем-то из ряда вон выходящим т.е. это хорошо известный инструмент, которым пользуются многие трейдеры/инвесторы. Настолько популярный, что его можно найти даже в мобильном приложении брокера. Несмотря на широкое распространение возникает вопрос: так ли она хороша и хороша ли вообще? Вот чтобы ответить на этот вопрос уже нужны руки из правильного места и владение техникой бектестинга. Бектестинг – это еще одна горячая тема разговоров с парнями из чатов. Все мы любим всякие модные штуки типа машин лернингов, бустовых деревьев, нейронок и прочих бигдатых бигдат, но нам не очень нравиться проверять эти модели на реальных данных потому как это требует усилий и часто сулит разочарованием.
Итак, краткое содержание всех букав далее: разбираемся в MACD, далее готовим бэктестинг и наконец считаем сколько можно было заработать честным трудом финансового спекулянта инвестора 😎
MACD 📈📉
Принцип работы модели достаточно простой: строится две экспоненциальные скользящие средние с разным окном, например, 12 дней и 26 дней. Далее считают разницу этих средних, которая и называется MACD. Уже на MACD накладывается еще одно скользящее среднее самой MACD, например с окном 9 дней. Очевидно, две итоговых кривые естественным образом где-то пересекаются. Собственно такие пересечения и являются:
- сигналом для покупки (сигнальная кривая пересекает MACD снизу)
- сигналом для продажи (сигнальная кривая пересекает MACD сверху)
Вот собственно и все, больше сказать особо нечего, но добавлю, пожалуй, иллюстрацию поярче из интернетов:
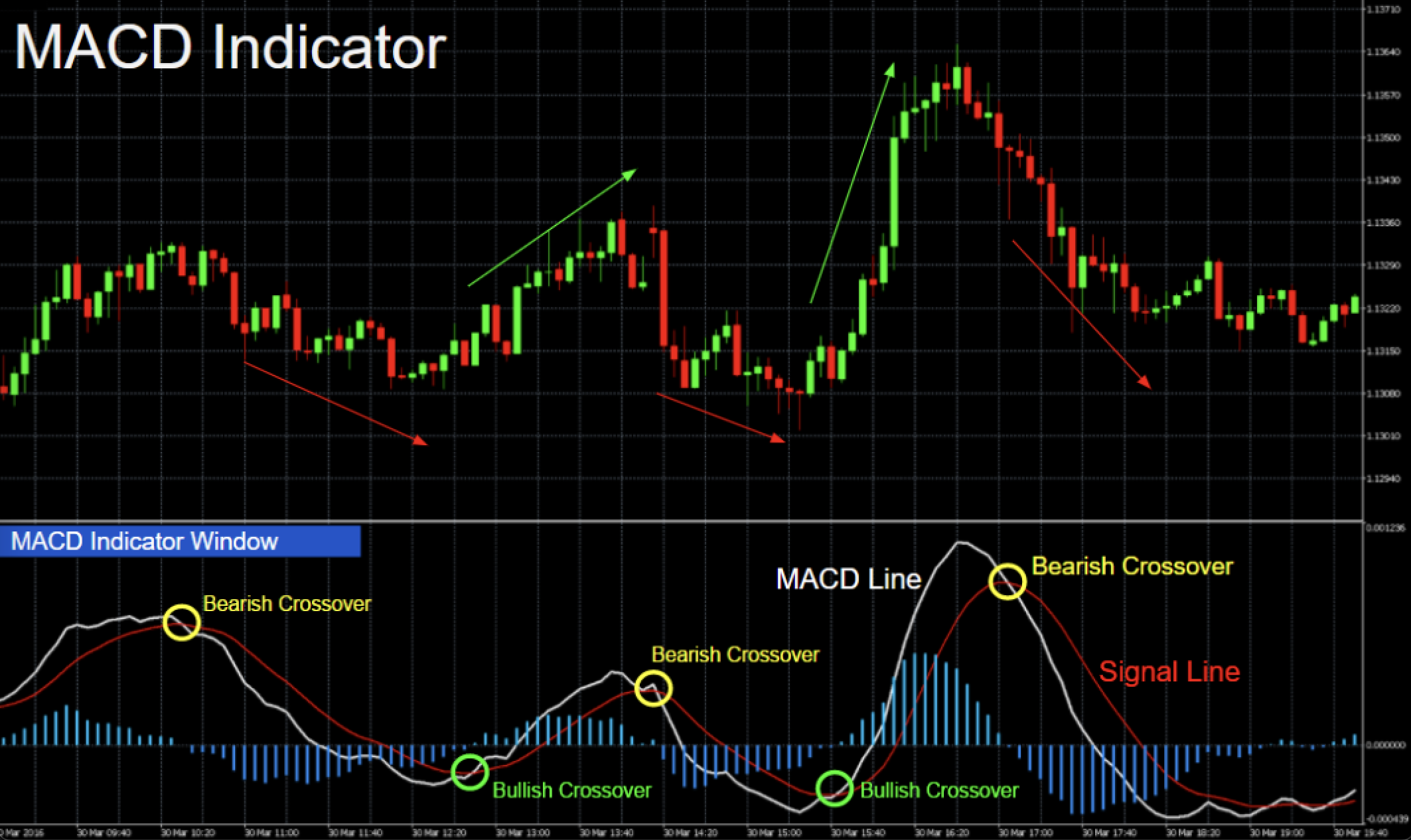Когда я много лет назад узнал об этой модели, у меня возник резонный вопрос: а собственно какого рожна я должен брать 12/26/9? Дело в том, что давным давно, когда люди на бирже записывали мелом цены сделок на доске, было принято торговать 6 дней в неделю. Кроме того, для истории фиксировались исключительно значения открытия и закрытия дня и посему фрейм записи сведений в то время был единственный – один день. Соответственно идея MACD была в том, чтобы ловить тренды для отрезка 2-х недель (12) и одного месяца (26). Сигнальная кривая выбиралась – 9 дней т.е. полторы недели. Сейчас такая конфигурация уже не является актуальной просто исходя из того как устроены торги на бирже.
Второй вопрос который у меня возник: а что собственно все это нагромождение усреднений означает? Пожалуй, прибегну к аналогии для объяснения феномена всех этих скользящих средних. Допустим, каждый день я прохожу некоторое количество шагов. Естественно, количество шагов меняется изо дня в день, и для наглядности я поставлю эту динамику в зависимость от женского настроения т.е. сделаю допущение, что каждые 30 дней все повторяется своим чередом с точностью до некоторой погрешности. Теперь можно воплотить этот простой паттерн в виде графика со всеми рюшами и кружевами, свойственным MACD: в частности, в качестве медленной средней я укажу 30 дней, а в качестве быстрой 15 дней и в качестве сигнальной 11 дней т.е. определю пропорцию 4(30):2(15):1.5(11), что соответствует или почти соответствует классической комбинации 12/26/9.
В качестве периодической функции был выбран cos(x), который показан белым пунктиром. Естественно, было добавлено немного грязи (случайной ошибки) в полученный набор данных, а конкретно в амплитуду и в фазу гармонической функции:
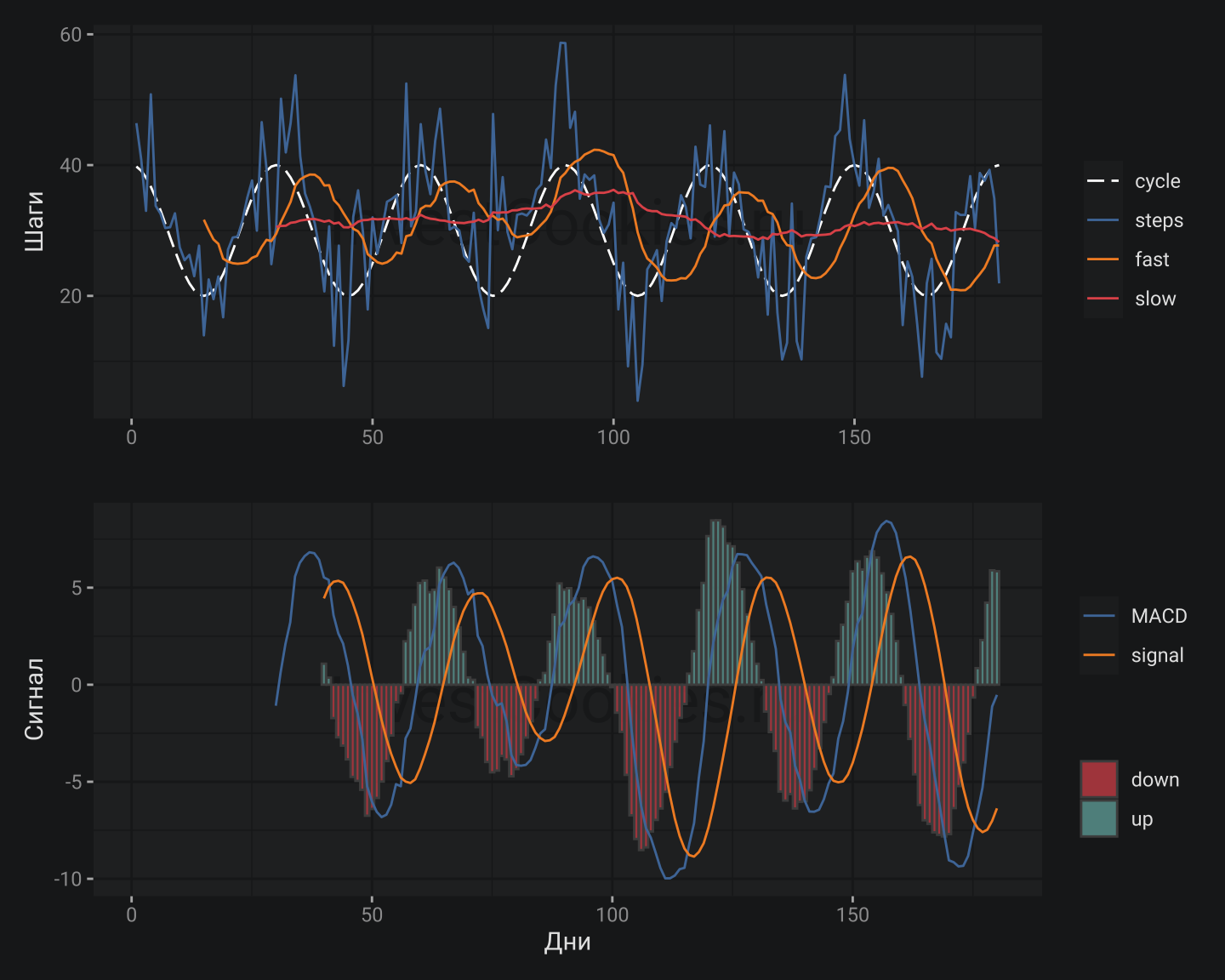
Можно заметить, что зеленые столбики на нижнем графике хорошо ложатся на верхние бугры циклической функции, а красные – соответственно на нижние. Получается, что пересечения нулевой отметки является вполне рабочим сигналом для прогноза роста или падения циклической динамики на 1/8 периода вперед.
Далее я уменьшу значение медленной средней в два раза - 15 дней, а пропорцию оставлю прежнюю: 4:2:1.5
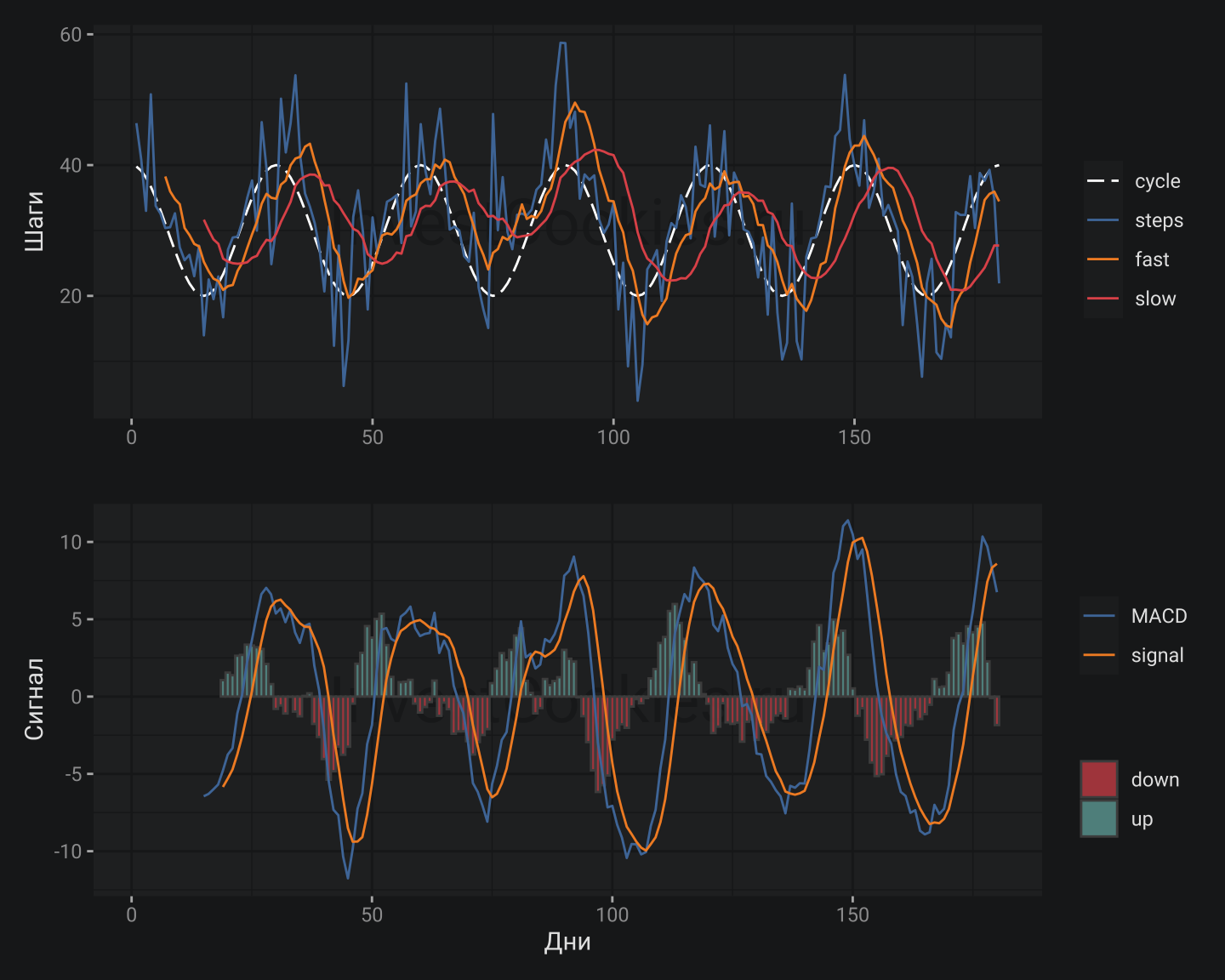
В данном случае MACD существенно изменилась: уверенность зелененьких и красненьких столбиков снизилась (появились выпадающие столбики) и также получилось смещение по фазе относительно варианта выше. Такое смещение дает возможность предсказать рост/падение уже на 1/4 периода, что собственно и было нужно. MACD фактически повторяет кривую шагов, а разница с сигнальной линии указывает на смену тренда. Данная комбинация условий хорошо укладывается в классическую концепцию использования MACD, когда сигналами для покупки/продажи выступают точки пересечения MACD/signal с нулевой отметкой. Формальная математическая формула для MACD с простой скользящей средней выглядит следующим образом: $$ MACD = \frac{\sum_1^n x_{i}}{n} - \frac{\sum_1^{2n} x_{i}}{2n} = 2\frac{\sum_1^n x_{i}}{2n} - \Big(\frac{\sum_1^{n} x_{i}}{2n}+ \frac{\sum_n^{2n} x_{i}}{2n}\Big) $$ $$ MACD=\frac{\sum_1^n x_{i}-\sum_n^{2n} x_{i}}{2n}, \quad 2n=15 $$
После некоторых преобразований получилось, что в данном случае MACD соответствует изменению числа сделанных шагов за 15 дней: в один день я мог сделать 20 шагов, а через 15 дней я уже сделал 40 шагов т.е. скорость изменений составила ~1.33 шага ежедневно. Можно повторить такую же операцию для разности MACD/signal и получить схожую интерпретацию. В обоих случаях речь будет идти о приращениях т.е. производных различного порядка, которые характеризуют скорость и ускорение. Другими словами, точки пересечения MACD/signal с нулевой отметкой – являются чем-то вроде графика производной 2-го порядка для динамики шагов, когда максимальные/минимальные значения достигаются в точке, где такая производная равна нулю. Все это совсем не удивительно, если вспомнить: $$ cos''(x)=-cos(x) $$
Наиболее популярной реализацией MACD связано с использованием экспоненциального сглаживания вместо обычного усреднения. Другими словами MACD можно записать следующим образом, если подставить формулу экспоненциального сглаживания для первого члена разности:
$$ EMA_{t}-EMA_{t-1}=\alpha P_{t} + (1-\alpha)EMA_{t-1} - EMA_{t-1} $$
Или после преобразований:
$$ EMA_{t}-EMA_{t-1}=\alpha (P_{t}-EMA_{t-1}) $$
[\alpha] – коэффициент сглаживания. Отсюда можно сделать вывод, что MACD соответствует отклонению значения в момент [t] от экспоненциально сглаженной средней предыдущих значений. Таким образом, вместо разности двух значений временного ряда в классическом определении производной используется разность между текущим значением и значением, полученным из всей совокупности предыдущих значений. Соответственно при [\alpha = 1] разность [EMA_{t}-EMA_{t-1}] превращается в обычное приращение т.е. разность текущего и предыдущих значений. Итак отличие лишь в том, что MACD с экспоненциальным сглаживанием обладает некоторой “памятью” о предыдущих значениях временного ряда.
Теперь я уменьшу значение медленной средней еще в два раза – до 8 дней при неизменной пропорции:
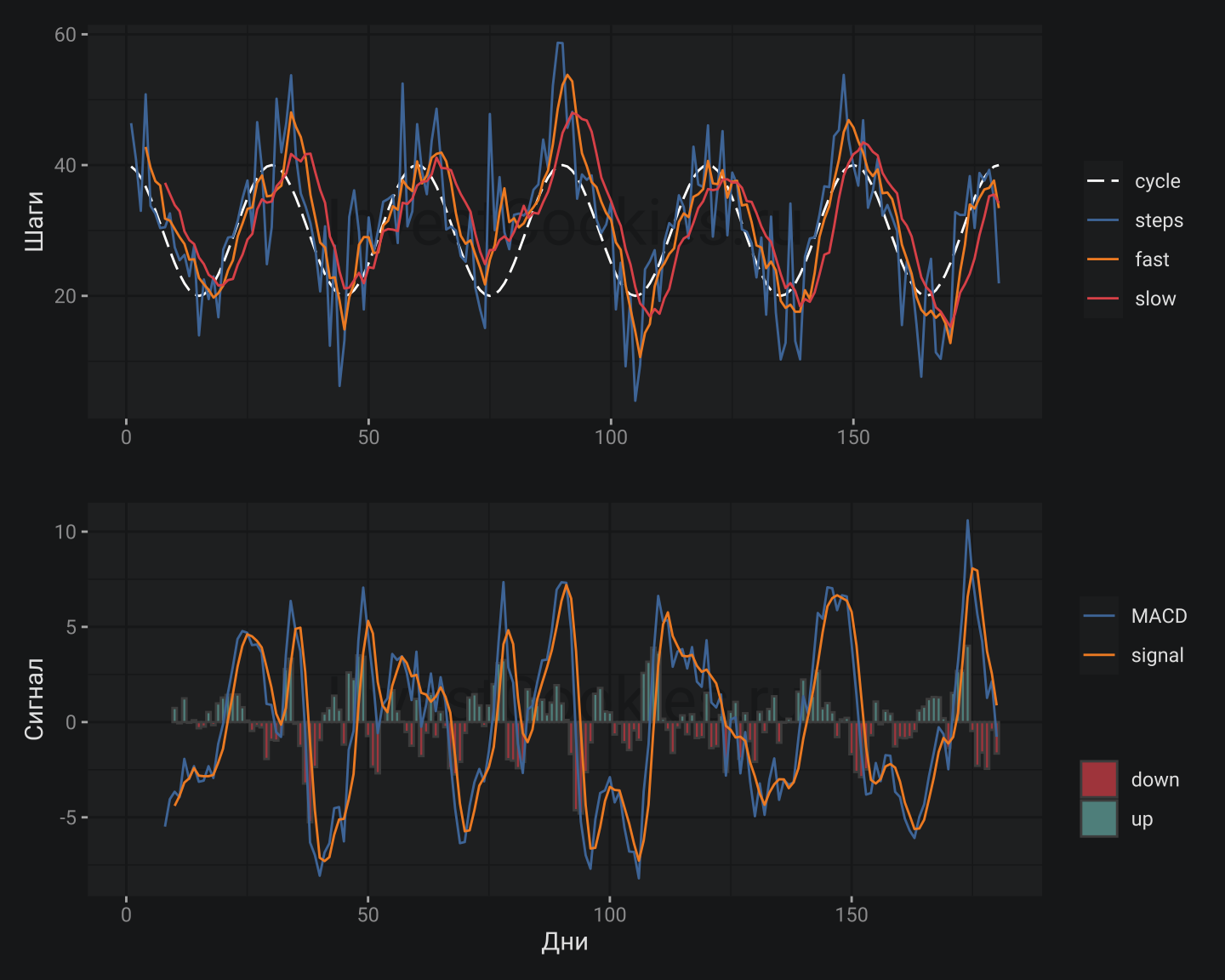
В данном случае модель существенно хуже справляется с задачей прогнозирования тренда и в целом обретает некую нервозность. Что же это означает? Очевидно, выбор параметров модели MACD влияет на ее способность к прогнозированию периодических функций. Впрочем, рыночные инструменты не сильно то и периодичны. В противном случае, простым Фурье-преобразованием можно было бы безошибочно предсказывать колебания цен на рыночные инструменты и быстро обогатиться.
Наконец, я увеличу значение медленной средней до 60 дней с прежними пропорциями:
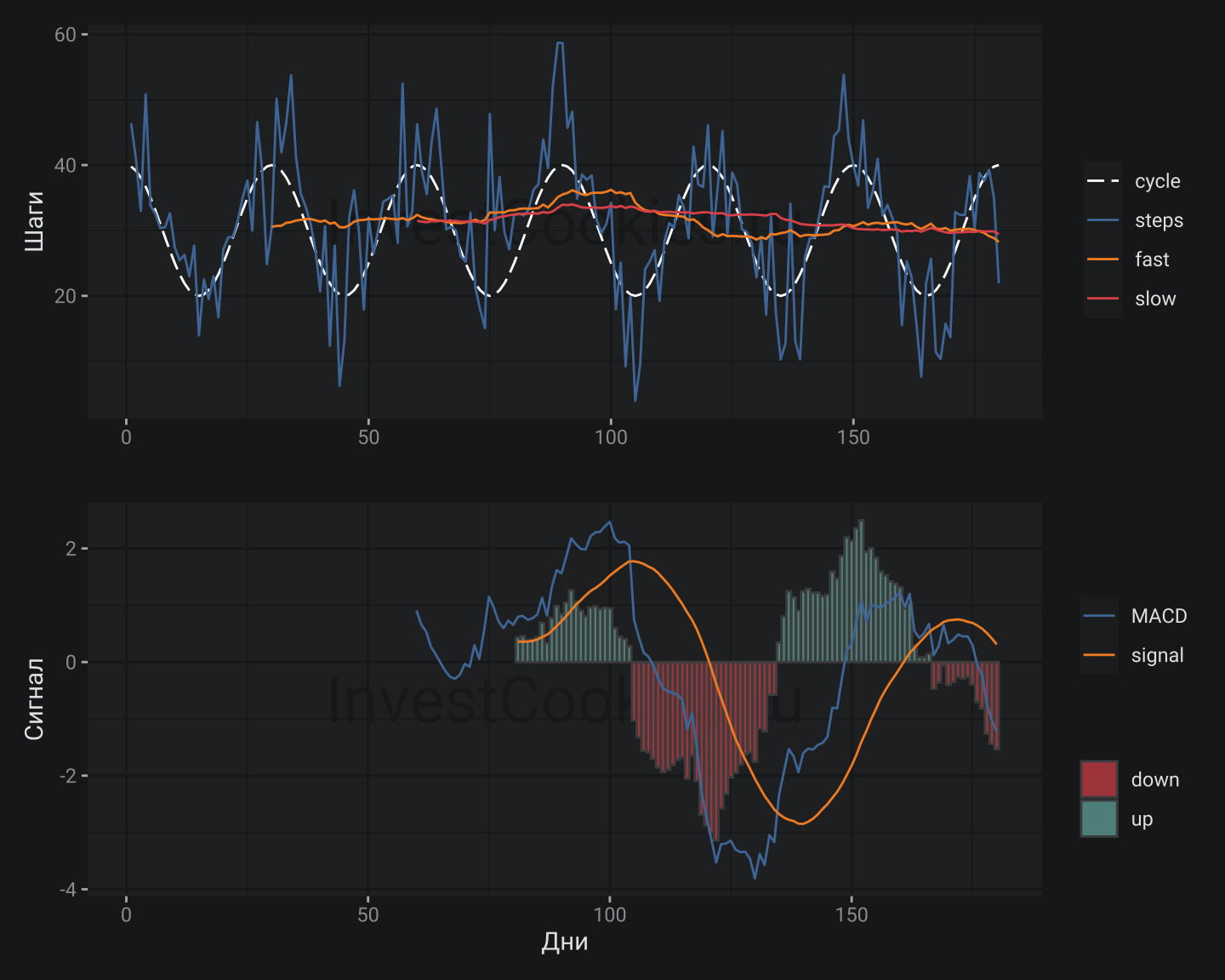
Увеличение периода также стало катастрофическим для прогнозной способности MACD. В одну фазу колебаний MACD уложилось сразу несколько исходных циклов, что сделало технику MACD бессмысленной в данном случае.
Выводы 🍪🍪🍪
Надеюсь, разобранные примеры и формальные пояснения позволили сформировать понимание, что из себя представляет MACD 🤘
Удалось получить формальную математическую интерпретацию этой техники в виде производной 2-го порядка или ускорения изменения цен, это наталкивает на выводы о том, что MACD будет хорошо работать на бумагах с длинными периодами роста или падения. MACD способен неплохо ловить точки смены тренда и соответственно черные лебеди и боковики – вот это все не очень желательно для MACD, исходя из концептуального понимания принципов работы техники. В теории, можно фокусироваться на голубых сырьевых фишках, которые ходят за долгосрочными трендами сырья. И тут сразу вспомнилась история с Газпромом, на который сначала налетел черный лебедь разрыва торговых отношений с Европой – основного рынка сбыта, а далее Газпром сам себе нарисовал черного лебедя с историей о дивидендах и “весело” об него убился окончательно 💥
Определенный параметры MACD способны захватывать колебательные паттерны благодаря тому что производная гармонической функции – является гармонической функцией. В любом случае, это свойство – является весьма бестолковым с учетом отсутствия явной периодичности у финансовых инструментов 🤦
В действительности, акции растут и падают не по гармоническим законам. При этом очевидно, что акции чаще растут чем падают. Дело в том, что совокупная капитализация рынков акций постоянно растет. Это связано с инфляцией и ростом мирового ВВП. С инфляцией, думаю, все понятно. Рост ВВП носит имманентный характер т.е. он встроен в рынок акций и будет продолжаться бесконечно. Ведь будет? Есть мнение, что рост мирового ВВП связан с постоянным увеличение населения планеты, но вроде как в ближайшие десятилетия этот рост остановится и мировая экономика войдет в новую доселе неизведанную территорию, бугага 👹
Но пока мировой ВВП растет можно продолжать отдавать предпочтение бычьим стратегиям, а не медвежьим. В любом случае, технику MACD стоит проверить для трендов роста и падения, которая будет непрерывно использовать наличествующий капитал для длинных и коротких позиций 🐂🐻
Этой заметкой я открываю серию, посвященную эффективности использования популярной стратегии торговли – MACD. В следующей заметке я подробно опишу как делать бектестинг для объективной проверки способности зарабатывать деньги на примере нескольких популярных акций. Код заметки на языке R под капотом 👇
Исходный код заметки
library(data.table)
library(ggplot2)
library(patchwork)
n <- 180
prd <- 30
set.seed(1982)
# Генерация примера с шагами на базе циклической функции с шумом
smp <- data.table(day = 1:n, cycle = cospi(1:n*2/prd)*10)[
, steps := 30 + cycle*rnorm(n, 1, 1) + rnorm(n, 1, 1)][
, cycle := 30 + cycle]
# Функция построения графиков
get_MACD <- function(smpl, k=30){
smp1 <- smp[, `:=`(fast=frollmean(steps, k/2), slow=frollmean(steps, k))][ # расчет скользящих средних
, MACD:=fast-slow][
, signal:=frollmean(MACD, k*3/8)][ # скользящая средняя для сигнальной кривой
, diff:=MACD-signal] |>
melt("day")
# График шагов
p1 <- smp1[variable %in% c("fast", "slow", "cycle", "steps")] |>
my_ggplot(aes(day, value, col = variable, lty = variable)) +
geom_line() +
scale_color_manual(values = c(cycle = "white", steps = my_pal[1], fast = my_pal[2], slow= my_pal[3])) +
scale_linetype_manual(values = c(cycle = 5, steps = 1, fast = 1, slow= 1)) +
labs(x = "", y = "Шаги", col = "", lty="")
# График MACD
p2 <- smp1[variable %in% c("signal", "MACD")] |>
my_ggplot(aes(day, value, col = variable)) +
geom_col(data = smp1[variable=="diff"], aes(fill = fifelse(value > 0, "up", "down")), col = "gray30", alpha=.7, size = .5) +
geom_line() +
scale_fill_manual(values = c("up" = my_pal[4], "down"=my_pal[3])) +
labs(x = "Дни", y = "Сигнал", col = "", fill = "")
p1/p2
}
get_MACD(smpl, 30) # медленная средняя 30 дней
get_MACD(smpl, 15) # медленная средняя 15 дней
get_MACD(smpl, 8) # медленная средняя 8 дней
get_MACD(smpl, 60) # медленная средняя 60 дней
Простой способ узнать о новых публикациях – подписаться на Telegram-канал: