А не пора ли нам подкрепиться?

Краткое содержание предыдущих серий

В заметке про Pointer Network было много всего: нетривиальная архитектура кодировщика (энкодера) и декодера, механизм внимания, а также совсем немного про обучение с подкреплением. В общем, много-много всякого, нужного для охвата пазла целиком. Далее в следующей заметке я начал растаскивать этот пазл по кусочкам и добавил интуиции вокруг механизма внимания, а теперь наступил момент поговорить подробнее про обучение с подкреплением.

Напомню, что современные архитектуры оптимизации, способные решать задачу коммивояжера, не нуждаются в правильных ответах, но могут самостоятельно изучать пространство возможных состояний и выбирать оптимальную стратегию достижения лучшего решения, используя оценки градиента функционала по параметрам стратегии. Здесь слово “функционал” – это тот редкий случай, когда оно употреблено к месту в отличие от более распространенной практики подмены слова “функциональность”.

Работая с задачами Data Science, мы как-то свыкаемся с идеей, что есть датасет с правильными ответами, и модель просто должна научиться корректно извлекать структуру для осуществления дальнейших прогнозов, будь то классификация или регрессионная оценка непрерывного показателя. Безусловно, на практике попадаются задачи кластеризации, поиска аномалий и снижения размерности, но такие задачи очень утилитарны, тогда как способность модели играть в видеоигры — это весьма убедительная имитация человеческого интеллекта.

Осознание этого факта в какой-то момент для меня стало откровением. В теме обучения с подкреплением ощущалась чёрная магия, а в голове шумели какие-то хаотические обрывки знаний про актёров и критиков, которые как-то умеют генерировать оптимальные решения для видеоигр или многострадального коммивояжера.

В этой заметке я попробую добавить немного интуиции в эту черную магию, зайдя в тему с главного входа, то есть путем реализации алгоритма Q-learning для задачи коммивояжера.

Q-функция

В первую очередь предлагаю определить законы, по которым будет жить не особо разнообразный мир коммивояжера. Скажем, например, что решения о посещении следующего города можно принимать на основании текущих состояний, то есть нахождения коммивояжера в некотором городе. Иными словами, процесс зависит только от текущего состояния и не связан с предыдущей историей. В таком случае говорят о марковском процессе. При этом, даже если мы используем masking, то есть игнорируем уже посещённые города, мы не делаем процесс менее марковским, так как решения по-прежнему принимаются исходя из текущего состояния и текущего знания об уже посещённых городах.

Соответсвенно, логично предположить, что задачу коммивояжера можно сформулировать в терминах марковского процесса принятия решения (Markov Decision Process, MDP):

[s] - текущее состояние или город, в котором сейчас коммивояжер
[s’] - новое состояние или город, который коммивояжер собирается посетить
[a] - действие для перехода из [s] в [s’]
[r] - награда, которую получает коммивояжер после перемещения из одного города в другой

Теория MDP разрабатывалась вокруг идеи научить искусственный интеллект играть в игры, поэтому большинство примеров проистекает также из видеоигр. В случае с TSP коммивояжер не кушает тортики и не бросается в лаву, как герой видеоигры, но перемещается из одного города в другой и получает награду [r := r(s,a)], или точнее штрафы в виде пройденного отрезка от одного города к другому.

Тогда процесс можно описать следующим образом. В начальном состоянии мира [s_0] коммивояжер находится в каком-то городе, возможно, в любом из доступных, но я на практике всегда помещаю в один и тот же город N-ск. Коммивояжер может наблюдать сразу все возможные города для следующего визита и на базе каких-то пока мистических ощущений, выбирает действие [a], которое считает лучшим (оптимальным). Мир отвечает коммивояжеру генерацией награды и коммивояжер оказывается в следующем городе и в следующем состоянии [s_1], далее процесс продолжается пока все города не будут посещены.

Введем понятие Q-функции для некоторой стратегии принятия решения [\pi]: $$ Q^\pi(s, a) := \sum_{t \geq 0} \gamma^t \mathbb{E}_{\mathcal{T} \sim \pi \mid s_0, a_0} [r_t] $$ По определению, Q-функция — это награды, которые коммулятивно набирает коммивояжер для всех траекторий (маршрутов) посещений [\mathcal{T}] городов, полученных из стратегии [\pi] для стартовых состояния [s_0] и действия [a_0]. Другими словами, коммивояжер посещает города, принимая решения на базе своей стратегии, и потом аккуратненько в эксельку записывает сколько он прошел (награду [r]), если был в таком-то городе и отправился другой. В следующий день он повторяет этот процесс, добавляя в эксельку, возможно какие-то другие сведения для других городов и действий, потому что решил посещать города немного в ином порядке.

Необходимо обратить внимание на весовой коэффициент [\gamma], который согласно теории должен быть меньше единицы (обычно от 0,9 до 0,99). Коэффициент [\gamma] обеспечивает уменьшение вклада будущих наград в Q-функцию. Такой параметр позволяет управлять склонностью получить награду прямо сейчас, нежели получить награды в будущем. Фактически, речь идет о выборе журавля в небе или синицы в руках. Его значение влияет на приоритет текущих наград перед будущими. Например:

Если [\gamma \to 0], коммивояжер ориентируется только на текущую награду.
Если [\gamma \to 1], коммивояжер учитывает долгосрочные награды.

В данном случае коммивояжер заносит в эксельку возможные решения, в какой город пойдет первым, получив первую награду [0.9^0r_1], далее – в какой город пойдет вторым получив награду [0.9^1r_2], и далее [0.9^2r_3], и таким образом выводит сумму, что и будет Q-функцией, которая представляет собой ожидаемую суммарную дисконтированную награду от действия [a] в состоянии [s], если следовать стратегии [\pi].

Получается, что коммивояжер бегает по городам, принимая решения на базе стратегии, которую пытается сделать оптимальной. Будем считать, что оптимальность стратегии [\pi] достигается, когда максимизируются награды по траекториям (маршрутам). Действительно, если такие маршруты дают нам хорошие или даже лучшие награды, то чего же еще желать? $$ \pi(s):=\underset{a}{\operatorname{argmax}} Q(s, a) $$

Табличный алгоритм

Соответственно, если у коммивояжера есть экселька и две переменные: состояния и действия [(s, a)], а также их возможные комбинации, то они могут быть аккуратно уложены в табличку вида:

	[s_1]	[s_2]	[s_3]
[a_1]	0	-50	-130
[a_2]	-10	0	-30
[a_3]	-40	-80	0

Здесь можно заметить, что использование таблички не является единственным доступным вариантом решения задачи. Вместо статичной записи, накопленных наград можно перейти к апроксимации Q-функции с использованием глубокого обучения. В таком случае на выходе получится архитектура DQN (Deep Q-learning). В то время как табличный метод подкупает своей простотой и наглядностью, DQN, очевидно, будет выглядеть более предпочтительно для задач большей размеренности.

Элементы в такой табличке инициализируются произвольно, например нулем, и означают награды коммивояжера, накопленные определенным образом, то есть с помощью формулы временной разности (Temporal Diﬀerence) для уравнения Беллмана: $$ Q_{k+1}(s, a) \leftarrow Q_k(s, a)+\alpha_k \underbrace{(\overbrace{r+\gamma \max_{a'}Q_k(s', a')}^{\text {target}}-Q_k(s, a))}_{\text {временная разность }} $$

, где [Q_k(s,a)] - это текущая оценка [Q^{\pi}(s, a)] на момент итерации

Несмотря на то, что данная формула имеет формальный вывод ее можно интерпретировать интуитивно. На каждом шаге совершается целевое (target) действие [a] по переходу из состояния [s] в состояние [s’], рассчитывается награда [r := r(s,a)], и извлекается [Q_k(s’,a’)] следующего состояния [s’] и следующего набора действий [a’], из которого выбирается лучшее (максимальное). Далее текущее приближение [Q_k(s,a)] просто сдвигается с некоторым коэффициентом (learning rate, скорость обучения) в сторону целевого (target) значения.

Формула на каждом шаге рассматривает фрагмент цепочки состояний и переписывает веса Q-матрицы, распространяя информацию о лучших наградах по цепочке по мере увеличения количества шагов. После того как маршрут определен, и корректировки Q-матрицы сохранены начинается новая итерация по поиску нового маршрута на базе обновленной Q-матрицы.

Последнее, что важно отметить – это преднамеренное нарушение стационарности стратегии принятия решений, то есть делается допущения об изменении стратегии с течением времени. Тогда идею поиска оптимального пути можно представить в виде дерева принятия решений, где ребра дерева представляют собой стоимость перехода (дистанция с обратным знаком или награда), а узлы - это состояния, в которые попадает коммивояжер. В узлах-состояниях такого дерева коммивояжер принимает решение о выборе города и это раскрывает перед ним новое состояние с новой конфигурацией выбора. Дерево решений не является частью алгоритма Q-обучения, но по-моему прекрасно объясняет проблему исследования всех возможных состояний задачи.

Сделав выбор в пользу траектории 1.4, коммивояжер получает максимальную награду (получает минимальный штраф за пройденную дистанцию) на первом этапе, но последующие решения не выглядят очень перспективными. Хотелось бы, чтобы коммивояжер заглянул во все состояния поддерева, а не жадно тыкался в траекторию 1.4, что в итоге позволило бы найти оптимальный маршрут 1.2.4.3. Чтобы позволить коммивояжеру исследовать потенциал других состояний нужно ввести две фазы работы алгоритма: исследование и эксплуатацию. Практическая реализация на R осуществляет плавный переход от режима исследования в режим эксплуатации приблизительно так:

if(runif(1) > epsilon){ # epsilon - затухающий с итерациями гиперпараметр 
        # ЭКСПЛУАТАЦИЯ
        q = Q_mtrx[,state] # выбор вектора состояния из Q-матрицы
        # mem - это простой вектор, который хранит информацию о посещенных городах
        q[mem] = -Inf  # игнорирование посещенных городов
        action = which.max(q) # выбор лучшего следующего решения
      }
      else{  
        # ИССЛЕДОВАНИЕ
        options = n_seq[which(!n_seq %in% mem)] # доступные для посещения города
        action = ifelse(length(options) == 1, options, sample(options, size = 1)) # случаный выбор города
      }

Еще один практический момент, который отличает конкретно мою реализацию от канонических вариантов, — это обработка терминального (конечного) состояния игры коммивояжера. По условиям задачи, коммивояжер должен вернуться в исходный город и получить последнюю награду для своего маршрута:

if(i == n_cities){ # если коммивояжер выбрал последний город для посещения
    # Q-табличка обновляется наградой перехода из последнего города в первоначальный
    Q_mtrx[action, state] = Q_mtrx[action, state] + 
      lr*(reward + gamma*next_q[mem[1]] -Q_mtrx[action, state])
  }else{ # иначе ...
    next_q[mem] = -Inf  # исключаем посещенные города 
    # Q-табличка обновляется выражением временной разности
    Q_mtrx[action, state] = Q_mtrx[action, state] + 
      lr*(reward + gamma*which.max(next_q) - Q_mtrx[action, state])
      }

Выражение для терминального состояния next_q[mem[1]] указывает на возврат коммивояжера в изначальный город.

В итоге получается алгоритм Q-обучения для задачи коммивояжера. Теория говорит о том, что данный алгоритм является off-policy, то есть не требуется отслеживать опыт взаимодействия конкретной стратегии со средой. На практике это дает приятное свойство обучать коммивояжера на любом опыте или на любых траекториях посещения городов, в том числе на траекториях другого коммивояжера, которые просто сохранены в буфер памяти. В принципе, даже не обязательно проходить полностью весь маршрут, достаточно просто исследовать все возможные состояния. В данной реализации это свойство не используется, по причине того, что извлечение траекторий для задачи TSP является простой процедурой, тогда как для многих иных игровых и бизнес-задач такой способ будет неприемлем. Действительно, на производственном предприятии никто не будет менять режимы производства для того, чтобы получить отклик среды специально для обучения модели с подкреплением. Куда вероятнее запустить алгоритм оптимизации на имеющихся исторических данных. Однако на этом преимущества такого подхода заканчиваются.

По сути, такой подход сводится к обучению критика в связке “актер-критик”, которая концептуально является основным понятием обучения с подкреплением. Действительно, в выражении временной разности есть только итеративная оценка Q-функции, говорящая о качестве текущей стратегии в явном виде через табличное представление.

Сопоставление с Pointer Network

Если вернуться в самое начало заметки и вспомнить про Pointer Network, а также формулу для оценки лосса: $$ L=-R⋅\sum_{i=1}^nlog(\rho(a_i)) $$

[R] - это награда всего маршрута
[(a_i)] - вероятность принятия действия с индексом [i]

Можно заметить, что награда представляет собой скалярный коэффициент, посчитанный для маршрута, а, собственно, градиент связан исключительно с вероятностями выбора действия, находящимися под логарифмом.

В данном подходе основной акцент делается на улучшении стратегии выбора действий, однако ничего не говорится об оценке этой стратегии, а также о Q-функции. Этот метод известен как REINFORCE. Его ключевая характеристика заключается в том, что он ориентирован на обучение актера – модели, способной непосредственно генерировать действия.

В отличие от этого методы Q-обучения и DQN сосредоточены исключительно на оценке действий, то есть в них работает только критик. В общем случае обучение с подкреплением сочетает обе эти составляющие:

Актера для обучения стратегии [],
Критика для обучения оценочной функции.

Вот такое получается “кино” с актерами и критиками, нужными для реализации обучения с подкреплением в общем случае.

Практическая реализация Q-обучения

Несмотря на то что весь искусственный интеллект в контексте Q-обучения уложился в 50 строчек кода на R, я буду придерживаться практики публикации исходного скрипта реализации в репозитории проекта AI Optimization. В этой заметке хотелось бы остаться на уровне идей и ключевых результатов. Базовая задача для анализа остается прежней – это случайно сгенерированные координаты 16 городов точно такие, какие использовались для всех предыдущих заметок серии.

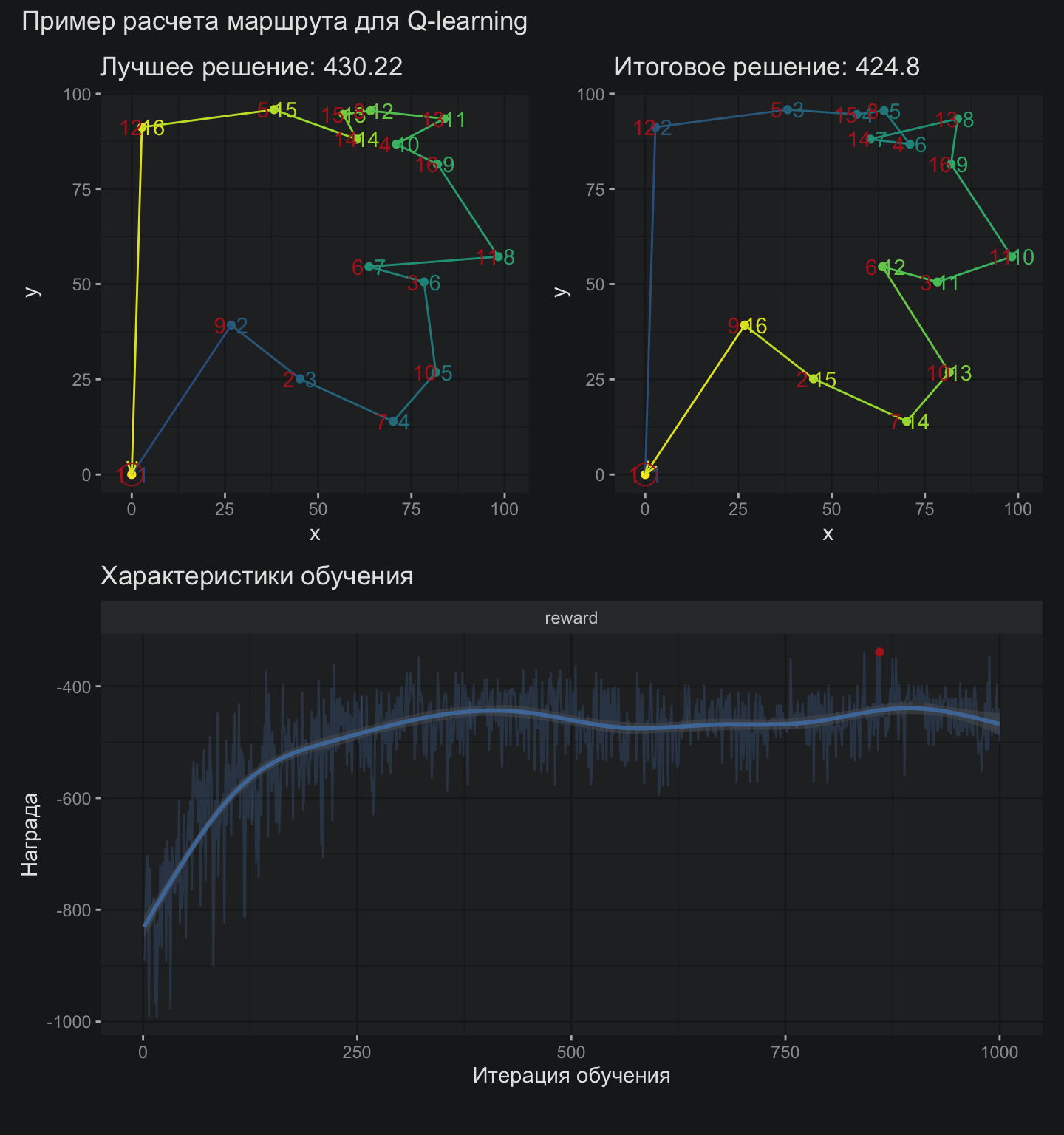
В данном случае лучший маршрут, который встречался в процессе обучения уступает маршруту, полученному из окончательной Q-матрицы, что в целом не является закономерностью. Кстати, матрица выглядит приблизительно так:

       V1  V2  V3   V4   V5   V6   V7   V8   V9  V10  V11  V12  V13  V14  V15  V16
1       0 -82 -83 -104  -88  -71  -62 -101  -45  -83 -151 -113 -168 -103 -102 -103
2     -39   0 -36  -59  -62  -34  -18  -58  -11  -30 -133  -70  -68  -61  -57  -54
3     -87 -33   0  -29  -46   -4  -35  -32  -51  -17   -5  -72  -32  -38  -35  -27
4    -103 -57 -27    0  -25  -31  -63    4  -64  -54  -30  -55    1   -6  -11   -9
5    -204 -70 -50  -18    0  -46  -78  -22  -46 -116  -70  -27  -36  -22   -5  -43
6     -72 -28  -4  -25  -37    0  -40  -37  -39  -26  -25  -70 -313  -29  -33  -31
7    -153 -18 -27  -65 -107 -313    0  -67  -44  -16  -50 -102  -75  -68 -105  -65
8    -106 -64 -41    2  -20  -38  -72    0  -66  -64  -36  -57   -4   -4    6  -20
9    -159 -16 -42  -57  -57  -37  -40  -63    0  -50  -71  -52  -73  -55  -55  -66
10    -73 -28 -18  -53  -67  -32  -15  -67  -44    0  -19  -95 -135  -61  -67  -42
11   -159 -55 -15  -32  -70  -34  -42  -37  -73  -28    0 -100  -38  -45  -42  -25
12    -78 -70 -76  -63  -35  -70 -101  -57  -55  -95 -100    0 -307  -43 -160  -67
13   -229 -70 -70   -6  -34  -43  -79  -16  -78  -60  -36  -80    0   -9  -22   -9
14   -188 -58 -36   -3  -12  -31  -65   -4  -57  -62  -46 -155  -19    0    0  -20
15   -108 -61 -43   -8   -7  -38  -72   -3  -56  -69  -40  -40  -13   -2    0  -24
16   -300 -60 -25   -4  -34  -32  -59   -8 -226  -48 -229  -79  -11  -17  -20    0

Напомню, что в данном случае колонки выступают в качестве состояния, а строчки в качестве действий. Соответственно, для определения траектории нужно пойти в первую колоноку и там найти максимальное значение. Номер строчки максимального значения и будет первым действие по переходу в другую колоноку. Небольшое залипательное кино по этому поводу:

Тестирование

В практическом отношении алгоритм Q-обучения может быть доработан по многим направлениям: можно поиграться с гиперпараметрами и скоростью обучения, добавить обучение из буфера. В данном случае я стараюсь придерживаться стандартных настроек и подходов в реализации алгоритма, иначе можно убить очень много времени на работу сомнительной перспективы. Тем не менее, сравнить алгоритмы хотя бы приблизительно – это то, чего я не готов лишиться после всего, что было тут написано.

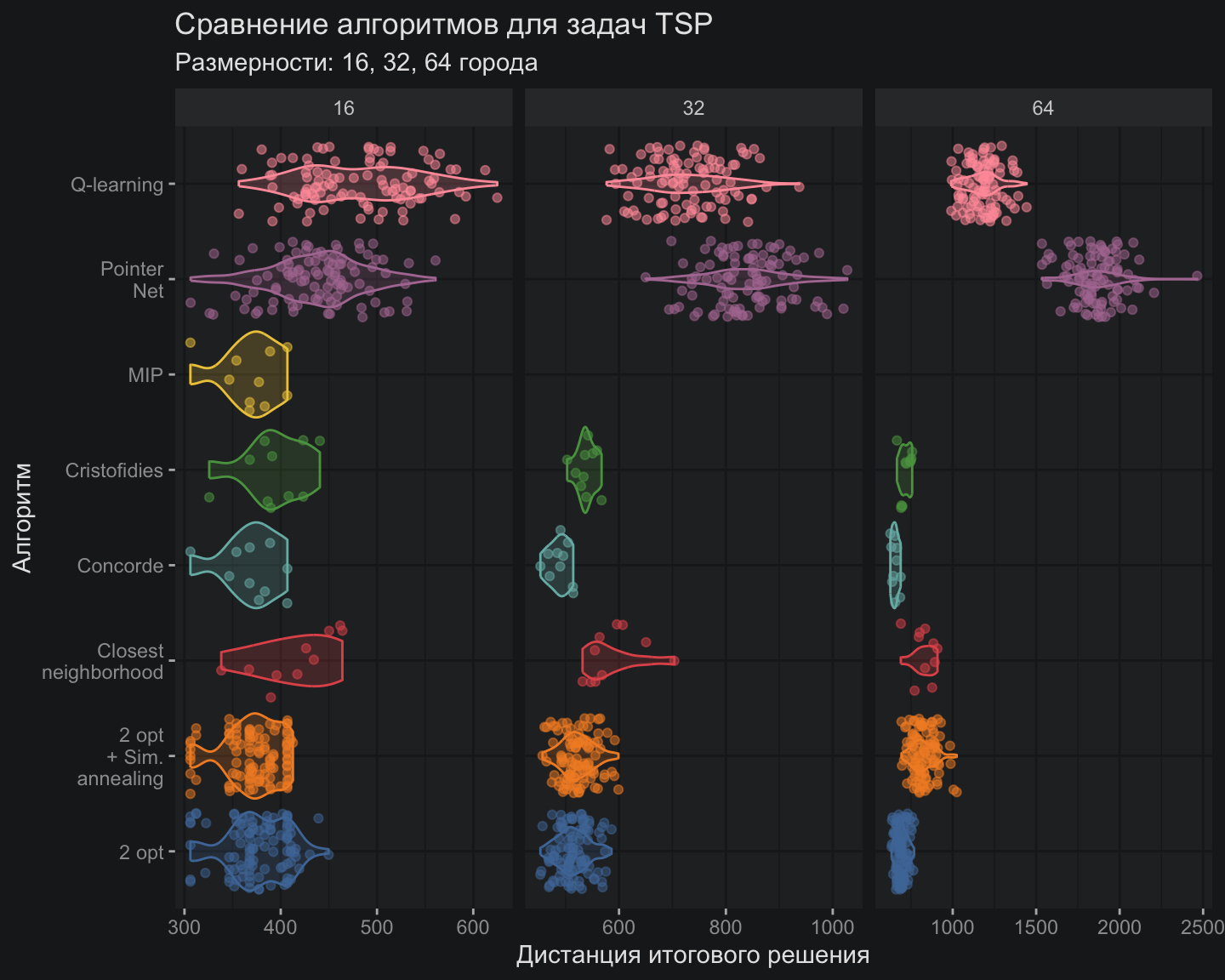
Теоретически Q-обучение в табличном виде должно не так хорошо справляться с задачами большой размерности, но в данном случае алгоритм выглядит предпочтительнее Pointer Net именно на размерностях более высокого порядка. Безусловно, все алгоритмы из мира ИИ пока выглядят гадкими утятами по сравнению с царь-алгоритмом Concorde или относительно простым Cristofides. Если посмотреть на вычислительную эффективность алгоритмов, то картинка для ИИ-алгоритмов выглядит не менее уныло:

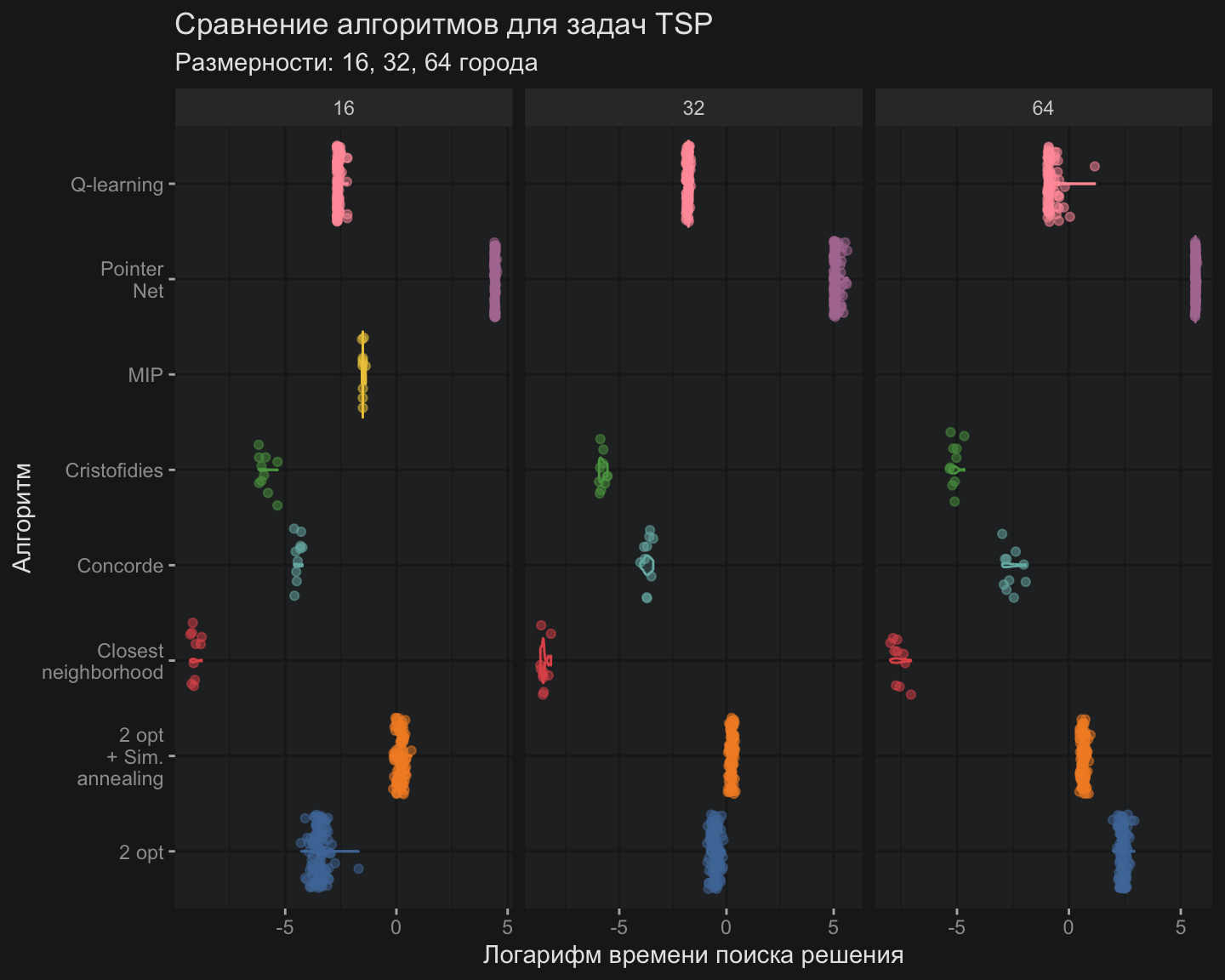
Путешествие по теории обучения с подкреплением и архитектурам нейронных сетей пока больше напоминает экстравагантное развлечение, а не доработку рабочего инструмента. Однако многие перспективные архитектуры пока еще не были рассмотрены в серии моих заметок. Есть надежда, что DQN и архитектура трансформеров смогут, если не превзойти классические алгоритмы по точности решения, то хотя бы приблизиться к ним, не теряя важной способности обобщения и оставаясь всеядными по отношению к широкому спектру задач оптимизации. Думаю, этих свойств будет уже вполне достаточно для старта обкатки таких алгоритмов в реальных производственных задачах.

Полезные ссылки:

Простой способ узнать о новых публикациях – подписаться на Telegram-канал:

🍪🍪🪙 InvestCookies

Краткое содержание предыдущих серий#

Q-функция#

Табличный алгоритм#

Сопоставление с Pointer Network#

Практическая реализация Q-обучения#

Тестирование#